Random variables X₁, X₂,…, X_n (each with ranges from−∞ to ∞) have a multivariate normal distribution if their joint probability density function (compare bivariate distribution) f is given by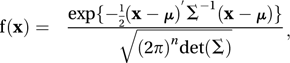where x is the n×1 vector of values, μ is the n×1 vector of means, Σ is the n×n variance–covariance matrix, and det(Σ) is the determinant of Σ.

For the special case of the bivariate normal distribution, with random variables X and Y, the joint probability density function f is given by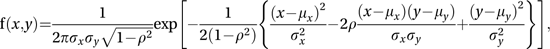where the mean and variance of X are μ_x and σ²_x, the mean and variance of Y are μ_y and σ_y², and ρ is the correlation coefficient between the two variables.