The theory that, in crystals, electrons fall into allowed energy bands, between which lie forbidden bands. Although free-electron theory can explain the electrical properties of metals, to understand fully the nature of electrical conduction, free-electron theory must be modified to include the effect of the crystal lattice in which the electrons move. Band theory modifies the free-electron treatment by including a regular periodic potential resulting from the positive ions in the lattice. Although the presence of the lattice alone does not give rise to electron scattering, except under special conditions, the periodic potential generated by the lattice does change the distribution of electron states given by the simple free-electron model.

In principle the original particle-in-a-box problem is modified by the addition of an extra potential term V(x, y, x), where V(x, y, x) has the same periodicity of the lattice it represents. The Schrödinger equation (see also quantum mechanics) that must be satisfied by these electron matter waves, ψ‎, is then:

where E is the energy of the state associated with ψ‎. Solutions to this equation are given by Bloch’s theorem.

As with the free-electron model, the equation above leads to a relationship between the momenta that characterize an electron state, and the energy of that state. However, this relationship is no longer the simple parabolic function:

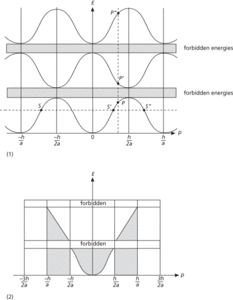
where p is the electron momentum that characterizes the state, and m is the mass of the electron. Instead the function is multivalued and there are certain forbidden bands of energy, i.e. no permitted states exist for them. The relationship between E and p for a one-dimensional crystal is shown in diagram (1).

The main feature is that all the curves repeat themselves over an interval in p of h/a, where h is the Planck constant and a is called the lattice constant. The electron states on the lower curve indicated by the points S, S′, and S″, are identical states except for their momentum values. The upper curves show that for each momentum value there are several permitted energies; one within each energy band (e.g. P, P′, P″). In order to avoid the confusion that would arise if the complete multivalued set of curves were used, it is conventional to choose certain sections of them in which as p increases so does energy E. The smallest values, starting from p=0, are reserved for the lowest energy band—the lowest curve in diagram (1). The next set from p=h/2a to h/a and −h/2a to −h/a is reserved for the second energy band (the middle curve in diagram (1), and so on. This zone structure is illustrated in diagram (2) and is called the extended zone scheme. It is merely a useful convention; any sets of p values that cover a range of h/a could be used to span all the available energy states.

A comparison of the extended zone scheme and the results of the free-electron model may easily be made by considering the relationship between E and p in the two models. This is shown in diagram (2) with the broken line corresponding to the free-electron parabolic relationship, E≅p².

The number of permitted values of p in each of the extended zones is equal to the number of ions in the crystal. As in the free-electron theory, each state corresponding to a value of p can take up two orientations of spin. So the total number of states in each zone is twice the number of ions in the lattice. This means that if the metal has only one electron per atom contributing to conduction, the electrons in the metal will only occupy all the states in the lower half of the zone—the shaded area in figure (2). No more than one electron can occupy any single state. This restriction on state occupation arises because electrons are fermions and therefore obey Fermi–Dirac statistics. For such a monovalent metal the energy distribution is virtually the same on the basis of either the free electron or band theory models, because the electrons have not started filling states beyond the first forbidden zone.

When the material has an even number of electrons per atom there would be an occupation of an integral number of zones. If an electric field were to be applied within the material, there would be a shift in the distribution of electron momenta that could only occur if and only if the zones are at close energy proximity. The electrons at the top of the uppermost filled zone can then obtain enough extra energy (e.g. from thermal excitations) to jump over the forbidden energy gap so that they can occupy permitted energy states at the bottom of the next zone. If this energy is very high compared with thermal energies, excitations to the next band cannot occur and there will be no current. The material would be classed as an insulator.

Band theory.

If the energy gap is not too large, a few electrons can absorb enough thermal energy to cross the forbidden energy gap. At room temperature thermal excitations are sufficiently large to breach this gap and to enable a small current to flow. Because the amount of excitation will increase with temperature, the conductivity will also increase with temperature. This behaviour is typical of a semiconductor.

Finally, elements with an odd number of electrons per atom are normally electrical conductors. This is because there are always unfilled states available within a given half-filled band. The electron momentum distribution within a band always looks like a small section of the free electron model for that particular extended zone. It is possible for elements with an even number of electrons per atom to be metals if there are bands that overlap in energy.