If Y1 has a non-central chi-squared distribution with ν1 degrees of freedom and non-centrality parameter λ, and if Y2 is independent of Y1 and has a chi-squared distribution with ν2 degrees of freedom, then the ratio X, where
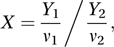 is said to have a non-central F-distribution with non-centrality parameter λ and with ν1 and ν2 degrees of freedom. The probability density function f of X is given by
is said to have a non-central F-distribution with non-centrality parameter λ and with ν1 and ν2 degrees of freedom. The probability density function f of X is given by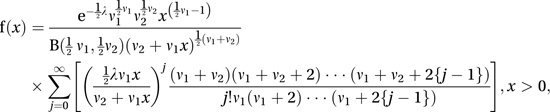 where B is the beta function. The distribution has mean and variance given by
where B is the beta function. The distribution has mean and variance given by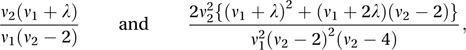 respectively (with ν2>4). The distribution is unimodal.
respectively (with ν2>4). The distribution is unimodal.
- growth line
- growth medium
- growth model
- growth pole
- growth rate
- growth ring
- growth substance
- growth triangle
- growth twinning
- groyne
- GRS
- Grubb, Howard (1844–1931)
- Grubbs catalyst
- Grubbs, Francis Ephraim (1913–2000)
- Grubbs test
- grue
- Grumman Aerospace
- grunerite
- Grunsfeld, John Mace (1958– )
- Grus
- grus
- Grzegorczyk axiom
- Grzegorczyk hierarchy
- grèze litée
- grèzes litées