If Z1, Z2,…, Zν are independent standard normal variables (see normal distribution) and δ1, δ2,…, δν are constants then X, given by
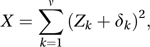 is said to have a non-central chi-squared distribution with ν degrees of freedom and non-centrality parameter λ, where
is said to have a non-central chi-squared distribution with ν degrees of freedom and non-centrality parameter λ, where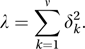 The probability density function f of X is given by
The probability density function f of X is given by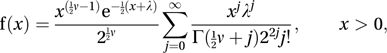 where Γ is the gamma function. The distribution, which is unimodal, has mean (ν+λ) and variance 2(ν+2λ). If λ=0 then the distribution becomes the chi-squared distribution with ν degrees of freedom.
where Γ is the gamma function. The distribution, which is unimodal, has mean (ν+λ) and variance 2(ν+2λ). If λ=0 then the distribution becomes the chi-squared distribution with ν degrees of freedom.
- Law, Bonar (1858–1923)
- Lawes, Sir John Bennet
- Law, John (1671–1729)
- lawlike
- lawnmower
- law of averages
- law of chemical equilibrium
- law of compound probability
- law of conservation
- law of conservation of energy
- law of conservation of mass
- law of constancy of interfacial angles
- law of constant composition
- law of constant proportions
- law of correlation of facies
- law of cross-cutting relationships
- law of definite proportions
- law of demand
- law of diminishing returns
- law of effect
- law of excluded middle
- law of faunal succession
- law of Haüy
- Law of Independent Assortment
- law of large numbers