A model of the atomic nucleus that has been successful in accounting for nuclear fission and the variation of nuclear stability with mass number. The density of a nucleus is independent of its size, which suggests that nuclear matter can be modelled on a drop of an incompressible liquid, such as water. Different excitation states of a drop-like nucleus can then be described in terms of spherical harmonics (see also normal modes). The success of the model has been associated with the fact that the binding forces in both the nucleus and the liquid drop are essentially short-ranged (see fundamental interactions). The liquid-drop model provides a subtle explanation for the variation of binding energy in different nuclei. Energy must be supplied to a drop of liquid in order to break it up into its component parts. For a drop of liquid, this energy is its latent heat of vaporization, which is proportional to the mass of liquid present. One would therefore expect a nucleus to have a binding energy proportional to its mass number. However, one needs also to offset this expectation by considering an effect analogous to the surface tension in the liquid drop. Nucleons (protons or neutrons) in the interior of a nucleus are attracted from all sides, whereas those at the surface are attracted only from within. The surface nucleons are therefore easier to remove and consequently have lower binding energies. In smaller nuclei, the surface nucleons form a greater proportion of the total volume than those in larger nuclei. It follows, therefore, that the binding energy is reduced by an amount proportional to the surface area of the nucleus. The binding energy will be further modified by the contribution of the electrostatic repulsion between protons, which will be significant for the larger nuclei (in which there are more protons). The nuclear model becomes a drop of positively charged liquid, whose stability is expected to be further modified by the internal motions of the protons and neutrons within it. Quantum mechanics can provide the form of this final contribution, which is often called a ‘symmetry term’ on account of its dependence on the difference of neutron and proton numbers (hence the tendency for the neutron number to equal the proton number in nuclei with low nucleon numbers). The liquid-drop model was originally proposed by George Gamow (1904–68) in 1928 and was revived by Niels Bohr and others in the 1930s after the discovery of the neutron.

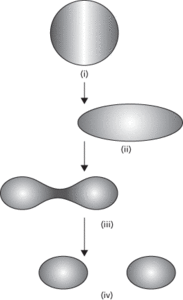
Liquid-drop model.