The branch of mathematics concerned with maximizing or minimizing a linear function subject to a number of linear constraints. It has applications in economics, industry, and commerce, for example. In its simplest form, with two variables, the constraints determine a feasible region, which is the interior of a polygon in the plane. The objective function to be maximized or minimized attains its maximum or minimum value at a vertex of the feasible region. For example, consider the problem of maximizing 4x1−3x2 subject to
The feasible region is the interior of the polygon OABCD shown in the figure, and the objective function 4x1−3x2 attains its maximum value of 17 at the point B with coordinates (5, 1).
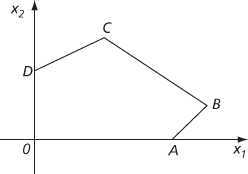
The feasible region
Often integer values are required, and in such cases the vertex is not always admissible and it will be necessary to test all points with integer values which lie close to the vertex. It is also possible that the objective function may be parallel to a constraining condition. In this case, all points on the boundary representing that constraint will be optimal.
A method for determining the optimal use of limited resources. The phrase ‘linear programming’ was used by Dantzig in 1949. A typical problem requires the maximization (or minimization) of a linear combination of the non-negative variables x1, x2,…, xn:
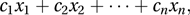 where the coefficients c1, c2,…, cn have known values. The function is known as the objective function. The maximization is subject to a set of linear constraints such as
where the coefficients c1, c2,…, cn have known values. The function is known as the objective function. The maximization is subject to a set of linear constraints such as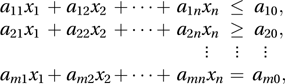 where the coefficients {aij} have known values.
where the coefficients {aij} have known values.In order to solve the problem, inequalities are turned into equalities by introducing non-negative slack variables so that, for example, the first inequality would become
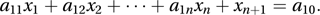
Any solution satisfying all the constraints (with the addition of slack variables as required) is called a feasible solution. A feasible solution involving exactly m non-zero x-variables (including any slack variables) is called a basic feasible solution.
One standard approach to the general problem is to use the simplex method (introduced by Dantzig in 1947). Special algorithms are required for integer programming (where the x-values are required to be integers) and for assignment problems, network flow problems, and transportation problems.
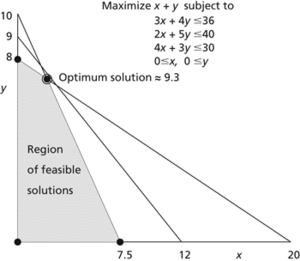
Linear programming. The solution must lie at one of the inner vertices marked with dots: these are the basic feasible solutions. The values of x+y at the other three vertices are 0, 7.5, and 8.
A mathematical technique used to provide an optimal solution to a set of linear equations. The technique uses a model of a process, which consists of a set of equations and also an objective function. The objective function may typically represent the economics of the process. The set of linear equations are known as constraint equations and define a region of feasibility that has an infinite number of solutions. The objective function is used to evaluate the optimal solution from these. Linear programming is widely used for process optimization, product supply and distribution, project management, and general resource allocation.
A technique in optimization, pioneered by George B. Dantzig, that is widely used in economic, military, and business-management decisions. It deals with the problem of finding nonnegative values of the variables x1, x2,…, xn that satisfy the constraints
and minimize the linear formMaximizing problems and problems with inequality constraints or unrestricted variables can be converted to this form. An optimum solution (if any exist) is known to be a basic feasible solution, which is one that satisfies the constraints and has at most m positive xi values.Computationally such problems are solved by the simplex method, an algorithm that terminates after a finite number of steps. It starts at a basic feasible solution and moves through the set of such solutions in such a manner that the value of the linear form is nonincreasing. Very large problems occur in practice involving sparse matrices. Iterative infinite algorithms are sometimes faster, notably Kamarkar’s method.
A mathematical procedure for finding the maximum or minimum value of a linear objective function subject to linear constraints.
- relative-time clock
- relative timescale
- relative URL
- relative volatility
- relative vorticity
- relativism
- relativistic beaming
- relativistic electronics
- Relativistic Heavy Ion Collider
- relativistic jets
- relativistic mass
- relativistic mechanics
- relativistic quantum mechanics
- relativistic quantum theory
- relativistic runaway theory
- relativistic speed
- relativistic velocity
- relativity
- relativity theory
- relaxation
- relaxation frequency
- relaxation oscillator
- relaxation time
- relaxation time(symbol: τ)
- relaxin