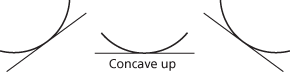
A real-valued function f is concave up (or convex) if the chord between any two points (a, f(a)) and (b, f(b)) on the graph y = f(x) always lies above the graph. If the second derivative f″(x) exists and is positive, then f is concave up. The graph of a concave up function lies above any tangent line to the graph. A function is said to be concave up at a value a if it is concave up on some neighbourhood of a.

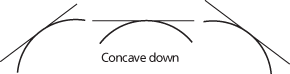
f is concave down (or just concave) if the chord between any two points (a, f(a)) and (b, f(b)) on the graph y = f(x) always lies below the graph. If f″(x) < 0 for all x, then f is concave down. The graph of f lies entirely below any of its tangents. A function is said to be concave down at a if it is concave down on some neighbourhood of a.