Laws that describe the way in which the sample mean approaches the population mean as the sample size increases. The phrase is due to Poisson, who, in 1835, referred to ‘La loi des grands nombres’. The weak law of large numbers states that if X₁, X₂,…, X_n are a set of independent identically distributed random variables, each with expected value μ, and if then, for every positive ε,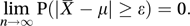An equivalent statement is that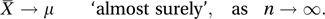

The strong law of large numbers states that, for every positive δ, it is always possible to find positive values ε and N such that

An equivalent statement is that

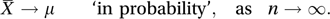
http://vis.supstat.com/2013/04/law-of-large-numbers/ Animation.