An effect observed in certain solids whose magnetic properties change at a certain characteristic temperature, T_N, known as the Néel temperature. Antiferromagnetism occurs in materials that have a permanent molecular magnetic moment associated with unpaired electron spins. At temperatures above the Néel temperature thermal agitation causes the spins to be randomly orientated throughout the material, which becomes paramagnetic: it obeys the Curie–Weiss law approximately but is characterized by a negative Weiss constant, θ, i.e.

where χ is the susceptibility and C a constant (see paramagnetism).

At temperatures below the Néel temperature interatomic exchange forces (see ferromagnetism) cause the spins to tend to line up in an antiparallel array. The susceptibility of the material depends on the crystalline structure, the temperature, and, in a single crystal, the direction of application of the external magnetic flux. In a single crystal of antiferromagnetic material, the antiparallel arrangement of spins can be considered as two interlocking sublattices, each spontaneously and equally magnetized in opposite directions (Fig. a). The sublattices may be represented by magnetic vectors M_A and M_B, each of which produces a flux experienced by the other. Thus the flux experienced by sublattice A may be represented as

where λ is a constant.

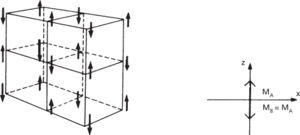
(a) Antiparallel arrangement of magnetic moments in simple cubic lattice The equivalent magnetization vectors

If an external magnetic flux density, B, is applied in a direction parallel to the direction of the spins, at temperatures near the Néel temperature the efficiency of the interaction is reduced by thermal effects: the spins are not all completely antiparallel so the material has a small positive magnetic susceptibility, χ_א, falling from a maximum at the Néel temperature as the temperature is reduced. At temperatures near absolute zero the antiparallel array becomes saturated due to the greater efficiency of the interaction and the susceptibility falls to zero (Fig. b).

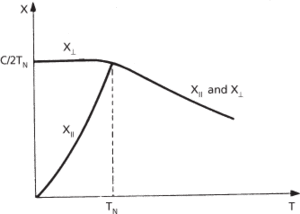
(b) Variation of susceptibility with temperature in a single antiferromagnetic crystal

If the magnetic flux is applied in a direction perpendicular to the spins, each magnetic vector turns towards B (Fig. c). The angle of rotation, α, is determined by the components of the magnetization vectors M_x and M_z and the components of flux B_x and B_z and is independent of the temperature. The overall magnetization of the specimen is 2M_x, where M_x is the component of each sublattice in the direction of B; it can be shown that

and that

where μ₀ is the permeability of free space and C the Curie constant from the Curie–Weiss law for the material. The susceptibility χ_א is thus equal to C₂T_N, i.e. it is not dependent on temperature below the Néel temperature (Fig. b).

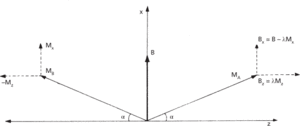
(c) Effect of external flux, B, applied perpendicular to magnetic moments

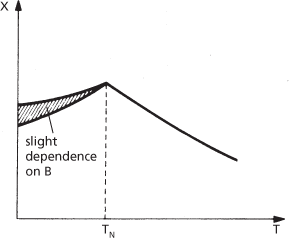
(d) Variation of susceptibility with temperature of polycrystalline specimen

The behaviour as described above assumes two equal sublattices. Some crystal structures, e.g. face-centred cubic, have more than two sublattices and the stable saturation array therefore may not be completely antiparallel; this leads to more complicated behaviour.

In a polycrystalline sample the susceptibility is a compromise between the two extreme conditions described above, with a small dependence on magnetic field strength at low temperatures, and antiferromagnetic materials are characterized by a maximum susceptibility at the Néel temperature (Fig. d).