A non‐parametric test for testing the null hypothesis that a given sample has been selected from a population with a specified cumulative distribution function F. Let x1, x2,…, xn be the sample values in ascending order, and let
If the null hypothesis is true, then z should be less than a value that can be obtained, for different significance levels, from tables.
A non-parametric test for the null hypothesis that a random sample has been drawn from a specified distribution (either discrete or continuous). There are several similar tests, each involving a comparison of the sample distribution function with that hypothesized. For example, let the sample values, in increasing order, be x(1), x(2),…, x(n). Let the hypothesized probability of a value less than or equal to x(j) be pj. Let uj and vj be defined by
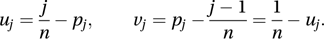The test statistic is the largest of the absolute magnitudes of these 2n differences. A two-sample version of the test compares the two sample distribution functions. In the single-sample case, approximate critical values are at the 5% level and at the 1% level. The test was introduced by Kolmogorov in 1933, and further developed by Smirnov in 1939.As described, the test refers to a fully prescribed distribution. However, by using special tables of critical values and estimating unknown parameters from the sample data, its use has been extended to testing for exponential, extreme-value, logistic, normal (the Lilliefors test), and Weibull distributions with unspecified parameters.
As an example, to test the hypothesis that the values 0.273, −1.184, 1.456, −0.655, −0.323, −0.733, −1.600, 0.819, 0.081, 0.971 have been drawn from a standard normal distribution the results given in the table are obtained.
value
j/n
pj
(j−1)/n
uj
vj
−1.600 x=10 a=27 b=87 w=0.25>
0.1
0.055
0.0
0.045
0.055
−1.184
0.2
0.118
0.1
0.082
0.018
−0.733
0.3
0.232
0.2
0.068
0.032
−0.655
0.4
0.256
0.3
0.144
−0.044
−0.323
0.5
0.373
0.4
0.127
−0.027
0.081
0.6
0.532
0.5
0.068
0.032
0.273
0.7
0.608
0.6
0.092
0.008
0.819
0.8
0.793
0.7
0.007
0.093
0.971
0.9
0.834
0.8
0.066
0.034
1.456
1.0
0.927
0.9
0.073
0.027
The value of the test statistic is 0.144, which is much less than 1.36/=0.41: so the null hypothesis is acceptable.