For a triangle, let M₁, M₂, M₃ denote the midpoints of the three sides. These three points define a circle known as Feuerbach’s circle or the nine-point circle. It gets its name because it passes through six further points of note. It passes through A₁, A₂, A₃, the three feet of the altitudes. The altitudes meet at the orthocentre O, and Feuerbach’s circle also passes through the midpoints of the line segments from the orthocentre to each vertex. The centre of the circle lies on the Euler line, halfway between the orthocentre and circumcentre. Further, Feuerbach’s circle touches the incircle and the three excircles of the triangle.

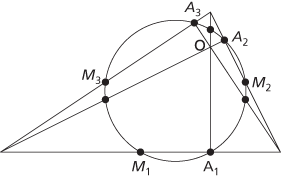
The nine points and circle