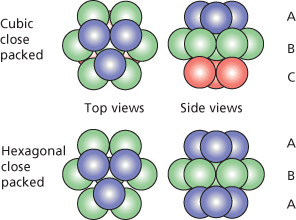
Now proven, the conjecture relates to optimal ways to pack spheres in three-dimensional space. The conjecture claims that the best ways are cubic close packing or hexagonal close packing, as shown in the figures. Each has a density of $\pi /\left(3\sqrt{2}\right)$, which is approximately 74%.

Optimal packings in 3d

Thomas Hales gave a computer-asssisted proof of the conjecture in 1998; at the time the proof consisted of 250 pages of mathematics and 3 gigabytes of data. By comparison, the optimal circle-packing arrangement in the plane was shown to be hexagonal packing in 1890 by Axel Thue; its density is π‎$/\left(\sqrt{12}\right)$, which is approximately 90.7%.