Let the complex numbers z₁ and z₂, where z₁ = a + bi and z₂ = c + di, be represented by the points P₁ and P₂ in the complex plane. Then z₁ + z₂=(a + c) + (b + d)i, and z₁ + z₂ is represented in the complex plane by the point Q such that OP₁QP₂ is a parallelogram; that is, such that $\overrightarrow{OQ}={\overrightarrow{OP}}_1+\overrightarrow{O{P}_2}$. In this way the addition of complex numbers corresponds exactly to the addition of vectors.

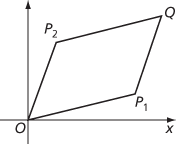
The parallelogram OP₁QP₂