A number that has a real part, x, and an imaginary part, iy, where i=√−1 and x and y are real (x can also equal 0). The complex number therefore has the form x+iy, which can also be written in the polar form rcosθ+irsinθ, where r is the modulus and θ is the argument (or amplitude). A complex number can be represented on an Argand diagram, devised by Jean Robert Argand (1768–1822), in which the horizontal axis represents the real part of the number and the vertical axis the imaginary part. In the polar form the modulus is the line joining the origin to the point representing the complex number and the argument is the angle between the modulus and the x-axis.
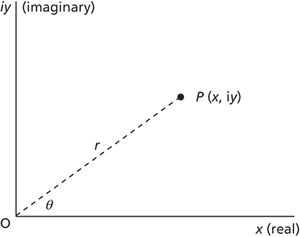
Complex number. Argand diagram.
There is no real number x such that x2 + 1 = 0. The introduction of an ‘imaginary’ number i such that i2 = −1 gives rise to the complex numbers a + bi, where a and b are real. The complex numbers subsume the real numbers (when b = 0). The set of all complex numbers is denoted ℂ. (The use of j in place of i is quite common.) Complex numbers can be added, subtracted, and multiplied as expected, remembering i2 = −1; for example:
Division by a non-zero complex number is also possible, noting: (see inverse of a complex number). The set ℂ of complex numbers in fact forms a field. More formally, the complex number a + bi can be identified with the ordered pair (a,b) of real numbers and arithmetic operations defined formally on such pairs in light of the previous calculations. See also argument, complex analysis, fundamental theorem of algebra, modulus of a complex number, polar form of a complex number.
A number that has a real and an imaginary part of the form x + jy where x and y are real, and . It can also be written in polar form as where r is the modulus and θ is the argument. Complex numbers are represented on an Argand diagram, and are useful in the study of the stability of controlled chemical processes.
A number that, for mathematical convenience, is regarded as being composed of two scalars (called the real and imaginary parts of the complex number), and is subject to a standard set of operations according to the rules of complex algebra.
In engineering, and especially control engineering and electrical and electronic engineering, complex numbers and complex operations are an essential tool without which calculations would be much more difficult to express and understand. Consequently, support for complex numbers and operations is an important consideration in the design of programming languages, packages, and libraries for use in engineering applications.
A number that can be written in the form x+iy, where x is its real part, y is its imaginary part, and i is the square root of −1. Complex numbers are a means to solve equations that require values that correspond to the square roots of negative numbers. They dramatically increase the number of mathematical problems that can be solved using polynomials, and have very natural interpretations in circuit theory as a representation of the phase of a.c. signals.
See number.
- THEOS
- theosophy
- therapeutic half-life
- therapeutic index
- therapsid
- Therapsida
- there exists
- therm
- thermal
- thermal analysis
- thermal battery
- thermal breakdown
- thermal bremsstrahlung
- thermal capacitance
- thermal capacity
- thermal cleaning
- thermal conductivity
- thermal cracking
- thermal death time
- thermal denaturation
- thermal diffusion
- thermal diffusivity
- thermal efficiency
- thermal emission
- thermal energy