See polar coordinates.
Suppose that three mutually perpendicular directed lines Ox, Oy, and Oz, intersecting at the point O, and forming a right-handed system are taken as coordinate axes. For any point P, let M be the projection of P on the xy-plane. Let r = |OP|, let θ be the angle ∠zOP in radians (0 ≤ θ ≤ π) and let ϕ be the angle ∠xOM in radians (0 ≤ ϕ < 2π). Then (r, θ, π) are the spherical polar coordinates of P. (The point O gives no value for θ or ϕ, but is simply said to correspond to r = 0.) The Cartesian coordinates (x,y,z) of P in terms of r, θ, and ϕ are given by
Compare cylindrical polar coordinates.
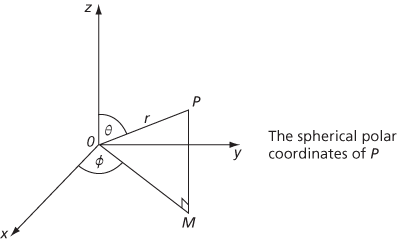
Coordinates that specify the location of a point in three dimensions. The basis of these coordinates is a set of three mutually perpendicular axes, Ox, Oy, and Oz, that intersect at O. Consider a point P, in three-dimensional space, at a distance r from O, the angle being equal to θ. Let OM be the projection of OP on the xy-plane and let the angle be equal to ϕ. The spherical polar coordinates of P are (r, θ, ϕ), where 0° ≤ θ ≤ 180°, 0° ≤ ϕ < 360°. These coordinates are related to the alternative Cartesian coordinates (x, y, z) by
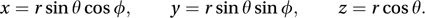
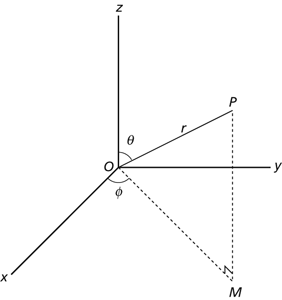
Spherical polar coordinates. Using Cartesian coordinates, the point P would be represented by (x, y, z), with x=r sin θ cos ϕ, y= r sin θ sin ϕ, z=r cos θ.
A technique for giving three-dimensional coordinates of a point based on its distance from a fixed origin and two angles relative to two perpendicular axes through that origin. The radial distance coordinate r can be interpreted as a move up the vertical z-axis, which is then followed by a rotation by polar angle θ down towards the horizontal x-axis, and finally a rotation by the azimuth angle φ about the z-axis towards the y-axis. There is no fixed convention as to the Greek symbols used for the two angles, so care is needed when using them. See also cylindrical polar coordinates; polar coordinates.
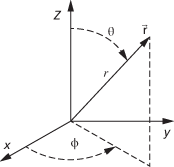
Spherical polar coordinates
- centre((in neurology))
- centreline
- Centre National d'Etudes Spatiales
- centre of calculation
- centre of curvature
- centre of gravity
- centre of inertia
- centre of mass
- centre of symmetry
- Centre Spatial Guyanais
- centre tap
- centric diatoms
- centric fusion
- centrifugal decanter
- centrifugal fan
- centrifugal force
- centrifugal forces
- centrifugal pump
- centrifuge
- centring
- centriole
- centripetal acceleration
- centripetal drainage
- centripetal drainage pattern
- centripetal force