The natural vibrations of an elastic sphere. Spherical harmonics may be used to describe the normal modes of oscillation of spherically shaped objects. They have been used mathematically to model systems as diverse as the surface of the sun and the atomic nucleus. They also occur in the solution of the Schrödinger equation for the hydrogen atom. Each harmonic has two identifying indices that distinguish it from other spherical harmonic waveforms. On the surface of a vibrating sphere, certain nodal circles appear, where the surface is at rest. The number of these nodal circles for a given spherical harmonic is called its order n; n is one of the indices used to identify the normal mode. The second identification index corresponds to the number m of nodal circles, which pass through the poles of the vibrating sphere. A general property of spherical harmonics is that if a nodal circle does not pass through the poles of the sphere, then it must lie in a plane parallel to the sphere’s equator. Consequently all nodal circles are lines of definite latitude or longitude.

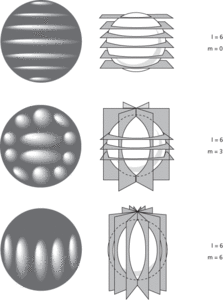
Spherical harmonics.