For a vector field v:ℝ²→ℝ², a singularity is a point p such that v(p) = 0. On a simple, closed, oriented (see orientation) curve C about p (which contains no other singularities), the direction of v wraps around the unit circle an integer number of times; that integer is the index of the singularity.

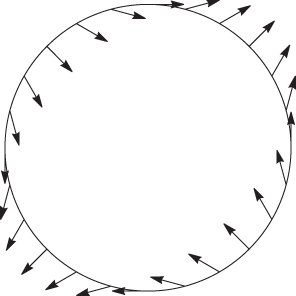
Singularity with index –1

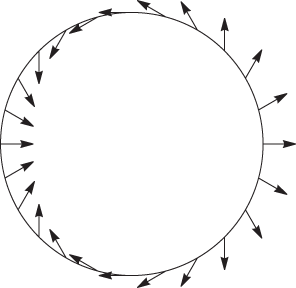
Singularity with index 2

For the first figure v(x,y) = (y,x), and (0,0) has an index of –1; note how the vector field goes anticlockwise once as we move clockwise around the circle. For the second field v(x,y) = (x²−y²,2xy), then (0,0) has index 2. This definition then generalizes to tangent vector fields on surfaces (see Poincaré-Hopf Theorem) and to higher dimensions (see degree (of a map)).