The generalization in n dimensions of a square in two dimensions and a cube in three dimensions.
In the plane, the four points with coordinates (±1, ±1) are the vertices of a square. In 3‐dimensional space, the eight points (±1, ±1, ±1) are the vertices of a cube. So, in n‐dimensional space, the 2n points with coordinates (x1, x2,…, xn), where each xi = ±1, are the vertices of a hypercube. Two vertices are joined by an edge if they differ in exactly one of their coordinates, and so there are n2n−1 edges. The vertices and edges of a hypercube in n dimensions form the vertices and edges of the graph known as the n‐cube.
In its simplest form, a four-dimensional cube, which can be considered as two three-dimensional cubes connected at equivalent corners. Connecting the corners of four-dimensional cubes gives a five-dimensional hypercube. In general, an (n+1)-dimensional hypercube can be generated by connecting the corners of n-dimensional hypercubes, and has twice as many corners as the n-dimensional hypercube.
Several multiprocessing systems have an architecture based on the hypercube, where processors replace corners and communication links replace edges. In an n-dimensional hypercube network, no processor is more than n links from any other processor; doubling the number of processors by using an (n+1)-dimensional network means information has to travel over only one additional connection. However, as the number of processors increases, the number of connections each one must make has also to be increased.
An interconnection network having the hypercube topology. (A hypercube in its simplest form is a four-dimensional cube, which may be considered as two three-dimensional cubes connected at equivalent corners.) The hypercube interconnection topology has 2N nodes (see diagram), such that each node has a unique binary address on the range 0 to 2N−1 and there is a direct connection between every two nodes whose addresses differ in exactly one bit position; N is the degree of the hypercube.
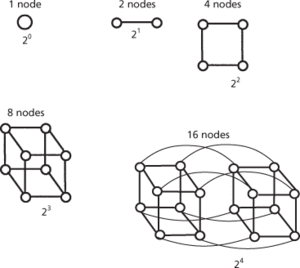
Hypercubes of different degrees
- market entry
- market equilibrium
- market failure
- market forces
- market for lemons
- market fundamentalism
- marketing
- market-maker
- market mechanism
- market potential
- market power
- market prices
- market risk
- markets
- market share
- market structure
- Markiewicz, Constance
- Markoffian process
- Markov, Andrei Andreevich (1856–1922)
- Markov, Andrey Andreyevich
- Markov chain
- Markov chain analysis
- Markov chain Monte Carlo
- Markov inequality
- Markovnikoff’s rule