Any of the functions hyperbolic sine (sinh), hyperbolic cosine (cosh), and hyperbolic tangent (tanh), and their reciprocals cosech, sech, and coth, defined as follows:
The functions derive their name from the possibility of using x = acosht, y = bsinht (tϵℝ) as parametric equations for (one branch of) a hyperbola. (The pronunciation of these functions causes difficulty. For instance, tanh may be pronounced as ‘tansh’ or ‘than’ (with the ‘th’ as in ‘thing’); and sinh may be pronounced as ‘shine’ or ‘sinch’. Many of the formulae satisfied by the hyperbolic functions are similar to corresponding formulae for the trigonometric functions, but some changes of sign must be noted (see Osborne’s rule). For example:
Since cosh(−x)=coshx and sinh(−x)= −sinhx, cosh is an even function and sinh is an odd function. The graphs of cosh x and sinh x are shown below.
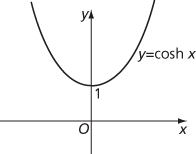
Graph of hyperbolic cosine
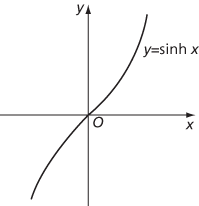
Graph of hyperbolic sine
The graphs of the other hyperbolic functions are:
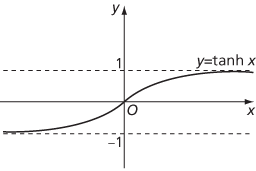
Graph of hyperbolic tangent
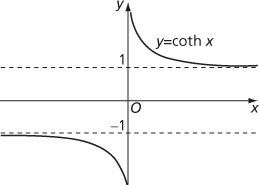
Graph of hyperbolic cotangent
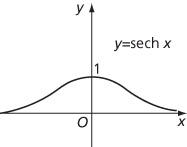
Graph of hyperbolic secant
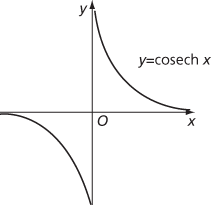
Graph of hyperbolic cosecant
The following derivatives are readily established:
See also inverse hyperbolic function.
- induction sonde
- inductive
- inductive coupling
- inductive effect
- inductive feedback
- inductive interference
- inductive load
- inductive logic
- inductively coupled plasma emission spectrometry
- inductive-output device
- inductive reactance
- inductive tuning
- inductor
- indulgence
- induration
- Indus
- Indus civilization
- indusium
- industrial action
- industrial cluster
- industrial concentration
- industrial democracy
- industrial dispute
- industrial district
- industrial diversification