An undesirable consequence (noted by Slutsky and by Yule) of applying a moving average to a time series. Suppose a time series consists of randomly chosen observations from the same population. We would therefore hope that any averaging would bring out

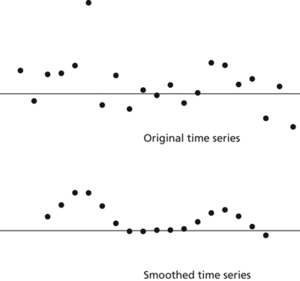
Slutsky–Yule effect. Chance variations in single values translate into apparent cycles in moving averages.

the fact that the mean was constant. However, by chance some values will be larger than others. Let x_k be a particularly large value. When we apply a moving average, all the averages that involve x_k will be inflated. With most moving averages the inflation will be greatest for the average centred on the kth observation and will diminish on either side. Each extreme value will have a similar effect such that the series of averages will present oscillations that appear real but are due to chance.