In an SIR epidemiology model, there are three mutually exclusive subsets of a constant population as a disease spreads: the fractions of the population that are susceptible S, infected I, and recovered R. A first such model was due to Kermack and McKendrick in 1927. The equations governing the model are

where α‎ is a positive constant relating to how contagious the disease is and the level of contact between people and β‎ is a positive constant relating to the rate of recovery. If cases grow, then the maximum value of I is an increasing function of R₀ = α‎/β‎, which is the expected number of people an infected person infects.

Such an SIR model makes accurate predictions for a disease spreading through a homogeneous closed population, but clearly the model does not take into account different demographics within a population, movement of people, mutation of the disease, catching the disease more than once, and responses from governments and society. There are many other so-called ‘compartmental models’ addressing some of these aspects.

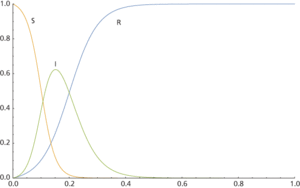
Graphs of S, I, and R in an epidemiology model