A form of periodic motion in which a point or body oscillates along a line about a central point in such a way that it ranges an equal distance on either side of the central point and that its acceleration towards the central point is always proportional to its distance from it. One way of visualizing SHM is to imagine a point rotating around a circle of radius r at a constant angular velocity ω. If the distance from the centre of the circle to the projection of this point on a vertical diameter is y at time t, this projection of the point will move about the centre of the circle with simple harmonic motion. A graph of y against t will be a sine wave, whose equation is y=rsinωt (see diagram). See also pendulum.
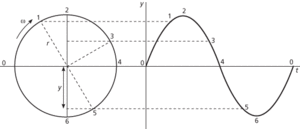
Simple harmonic motion.
Suppose that a particle is moving in a straight line so that its displacement x at time t is given by x = Asin(ωt+α), where A>0, ω, and α are constants. Then the particle is exhibiting simple harmonic motion, with amplitude A, period 2π/ω, and phase α. This equation gives the general solution of the differential equation
An example of simple harmonic motion is the motion of a particle suspended from a fixed support by a spring (see Hooke’s law). Also, the motion of a simple pendulum performing oscillations of small amplitude is approximately simple harmonic motion.
- triangular distribution
- triangular facet
- triangular irregular network
- magnetic transition temperature
- magnetic trap
- magnetic tuning
- magnetic variable
- magnetic variation
- magnetic variations
- magnetism
- magnetite
- magnetization
- magnetization curve
- magnetization(symbol: M; unit: ampere per metre)
- magnetize
- magnetizing force
- magneto
- magnetobremsstrahlung
- magnetocaloric effect
- magnetochemistry
- magnetochronology
- magnetoelectronics
- magnetoencephalography
- magnetogram
- magnetograph