In coordinate geometry, suppose that A and B are two points on a given straight line, and let M be the point where the line through A parallel to the x‐axis meets the line through B parallel to the y‐axis. Then the gradient of the straight line is equal to MB/AM. (Notice that here MB is the measure of $\overrightarrow{MB}$ where the line through M and B has positive direction upwards. In other words, MB equals the length |MB| if B is above M, and equals −|MB| if B is below M. Similarly, AM = −|AM| if M is to the right of A, and AM = −|AM| if M is to the left of A. Two cases are illustrated in the figures.)

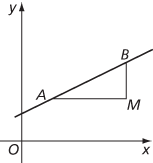
B is above A

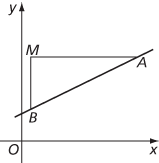
B is below A

The gradient of the line through A and B may be denoted by m_AB, and, if A and B have coordinates (x₁, y₁) and (x₂, y₂), with x₁ ≠ x₂, then

Though defined in terms of two points A and B on the line, the gradient of the line is independent of the choice of A and B. The line in the figures has gradient $\frac{1}{2}$.

Alternatively, the gradient may be defined as equal to tanθ‎, where either direction of the line makes an angle θ‎ with the positive x‐axis. (The different possible values for θ‎ give the same value for tanθ‎.) If the line through A and B is vertical, that is, parallel to the y‐axis, it is customary to say that the gradient is infinite. The following properties hold:

1. (i) Points A, B and C are collinear if and only if m_AB = m_AC. (This includes the case when m_AB and m_AC are both infinite.)

2. (ii) The lines with gradients m₁ and m₂ are parallel if and only if m₁ = m₂. (This includes m₁ and m₂ both infinite.)

3. (iii) The lines with gradients m₁ and m₂ are perpendicular if and only if m₁m₂ = −1. (This must be reckoned to include the cases when m₁ = 0 and m₂ is infinite and vice versa.)