A measure of the variability of a set of data. For data x₁, x₂,…, x_n, with sample mean given by 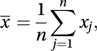the sample variance is defined to be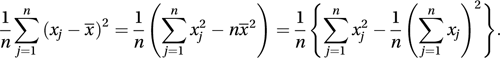The variance is never negative and can be zero only if all the data values are the same.

In the case where the frequency of the observation x_j is f_j, for j=1, 2,…, m, the variance can be calculated using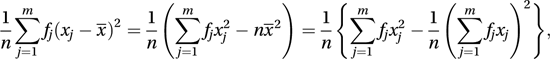where n, the total sample size, is given by 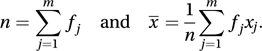In these expressions for variance the divisor n is used. This is correct if the data set effectively constitutes the entire population; for example, if the values x₁, x₂,… are the diameters of the planets of the solar system, or the lifetimes of all known patients with a rare disease. However, if the data constitute a random sample from a population, and we are interested in the variance of the values in the population, as opposed to the variance of the values in the sample, then it is appropriate to use the divisor (n−1), since this leads to an unbiased estimate of the population variance. This sample variance is given by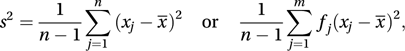as appropriate. The factor linking the population variance formulae and the sample variance formulae is known as the Bessel correction.