The number line ℝ, plane ℝ2, and 3‐dimensional space ℝ3 can be generalized to n‐dimensional Euclidean or Cartesian space ℝn with coordinates (x1, x2,…, xn) on which the operations of addition and scalar multiplication are extended in the obvious way. While ℝn is hard to visualize for n>3, it provides a powerful framework in linear algebra and multivariable analysis.
If the points P and Q have coordinates (x1, x2,…, xn), and (y1, y2,…, yn) respectively, then the distance PQ can be defined to be equal to
Sometimes n‐dimensional Euclidean space is denoted as En, signifying that space has no predetermined coordinates, no natural origin or axes. Once an origin, perpendicular axes, and unit length have been decided, coordinates may be assigned and En can now be identified with ℝn.
A term used to describe ordinary two- or three-dimensional space. Also used in connection with the n-dimensional space Rn, in which a point is a real column vector x = (x1 x2…xn)′, the distance between two points x and y is
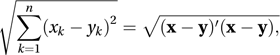 and the angle θ (0 ≤ θ ≤ π) between the vectors x and y is given by
and the angle θ (0 ≤ θ ≤ π) between the vectors x and y is given by 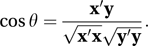
- reeve
- reference
- reference ellipsoid
- reference frame
- reference point
- reference section
- reference star
- reference template
- referent
- referential integrity
- referentially opaque/transparent
- referential opacity
- referential transparency
- referer
- referrer
- refertilization
- refine
- refined boxplot
- refinement
- refinery
- refinery gas
- refining
- reflation
- reflectance
- reflectance function