A versatile non-parametric test. One application is as a test of the null hypothesis that two samples, of sizes m and n, have been taken from random variables with the same distribution. Arrange the two sets of observations in joint order from least to greatest. Label the observations 1 or 2 according to their sample. This results in a sequence of 1s and 2s, e.g. 1–222–1–2–1111–2–1, containing a number of runs (in this case, seven). If there are too few sequences (e.g. 1111111–22222), then this leads to rejection of the null hypothesis. The test statistic is the number of runs. Under the null hypothesis, for reasonably large m and n, this has an approximate normal distribution, with mean and variance equal to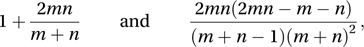respectively. Since the count is an integer, a continuity correction of 0.5 will be needed.

As an example, suppose that the reaction times, in ms, of 20 girls and 25 boys were:

Girls  428, 444, 446, 479, 492, 513, 522, 533, 544, 545, 560, 566, 581, 582, 590, 595, 599, 612, 634, 655

Boys  415, 439, 442, 477, 500, 512, 523, 532, 577, 580, 613, 614, 622, 633, 670, 671, 680, 688, 701, 703, 722, 730, 744, 750, 777

The null hypothesis is that the reaction times are independent samples from a common distribution, the alternative hypothesis being that this is not the case. Denoting the boys by 2s, we get the sequence

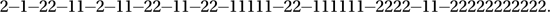
There are therefore just fifteen runs. The resulting z-value is 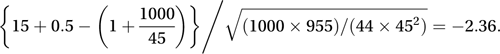The corresponding tail probability (see tail area) is about 0.009. Considering both tails, the probability is 0.018 and this provides strong evidence to reject the null hypothesis.