If X is a random variable with pdf given by where Γ is a gamma function and λ, v, x are all positive, then we say that X has a gamma distribution with parameters λ, v. When v = 1, f(x) reduces to λe−λx which is the exponential distribution.
The general form of the gamma distribution has probability density function f given by
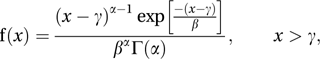where α ( > 0), β ( > 0) and γ are parameters, and Γ is the gamma function. The distribution has mean αβ+γ and variance αβ2. If α>1 then the distribution has mode at x = γ+β (α−1); otherwise the mode is at x = γ.The case (α = ½, β = 2, γ = 0) corresponds to the chi-squared distribution with ν degrees of freedom. The case (β = 1, γ = 0) gives the standard form of the distribution:
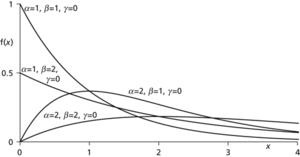
Gamma distribution. For simplicity γ = 0 for all the illustrated cases, which have mean αβ. When α ≥ 1 the mode is at x = β(α−1), otherwise it is at α = 0.
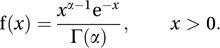The case (α = 1, β = 1, γ = 0) gives the exponential distribution, and the case (α = k, β = 1, γ = 0), where k is a positive integer, gives the Erlang distribution, which is the distribution of the time to the kth event in a Poisson process. If Z is a standard normal variable (see normal distribution) then ½Z2 has a gamma distribution with parameters α = ½, β = 1, γ = 0.
A continuous distribution with a density function of the form
for 0 ≤ x < ∞ and α,β > 0, and the moment generating function for t<1/ β. The gamma distribution has mean αβ and variance αβ2. Important special cases are the exponential distribution (α = 1) and the chi-square distribution (α = n/2, β = 2). The gamma distribution is also related to the Poisson distribution: if X is a gamma (α, β) random variable with integer α and Y is a Poisson (x/β) random variable, then P[X ≤ x] = P[Y ≥ α].