A classic random walk problem that can be solved using the theory of Markov processes. At each play a gambler is supposed to have probability p of winning one unit and probability q (= 1−p) of losing one unit. The gambler starts with j units. Betting continues until either the gambler's fortune reaches N (in which case the gambler retires) or the gambler is ruined. If p = ½ then the probability of ruin is 1−(j/N), and otherwise it is
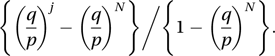
- Togo
- Tojo Hideki (1884–1948)
- Tokamak
- tokamak
- Tokarev, Valery Ivanovich (1952– )
- token
- token bus
- token card
- token money
- token-reflexive
- token ring
- token-token identity
- Tokugawa
- Tokugawa Ieyasu (1542–1616)
- Tokugawa Yoshimune (1684–1751)
- Tokyo Round
- Tokyo Trials
- Toland, John (1670–1722)
- tolerable risk
- tolerance
- tolerance interval
- toleration
- Toleration Act (1689)
- Tollens reagent
- Toll-like receptor