A technique for making multivariate data easier to understand. Suppose that there is information on n variables for each data item. These variables are unlikely to be independent of one another; a change in one is likely to be accompanied by a change in another. The idea of PCA is to replace the original n variables by m (<n) uncorrelated variables, each of which is a linear combination of the original variables, so that the bulk of the variation can be accounted for using just a few explanatory variables. In the diagram overleaf, the two original variables x₁ and x₂ can be replaced by the first principal component, y₁.

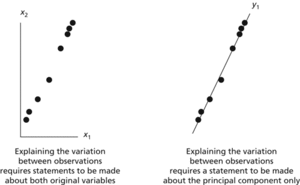
Principal components analysis. Principal components analysis aims to explain an n-dimensional situation using m (<n) uncorrelated variables. Here n=2 and m=1.

Let R denote the correlation matrix for the case of p x-variables. The coefficients of the x-variables corresponding to the kth principal component are the elements of the eigenvector corresponding to the kth largest eigenvalue, λ_k, of R. All the eigenvalues are real and non-negative, since R is positive semi-definite. The proportion of the variation in the data explained by the kth principal component is . The first few principal components should account for the majority of the observed variation. The hope is that the linear combinations thus identified will have some natural interpretation. The Kaiser rule proposes that only components having eigenvalues greater than unity should be retained. See also scree plot.