The frequency at which resonance occurs in a particular circuit or network. Resonance occurs in a circuit containing both capacitance and inductance when the imaginary component of the complex combined impedance of the circuit is zero, i.e. when the supply current and voltage are in phase and the circuit has unit power factor.
In a series resonant circuit, which contains the capacitive and inductive elements in series (Fig. a), the combined impedance, Z, is given by
where R is the ohmic resistance, ω the angular frequency (ω = 2π × frequency), L the inductance and C the capacitance, and j equals √−1. The resonance condition is fulfilled when
i.e. when
In a series resonant circuit resonance occurs therefore when the combined impedance is purely resistive and is a minimum. The resistance can be low even for large values of L and C. In this case the current flowing through the circuit will be high, and although large voltages are developed across the individual elements these are out of phase with each other so that the total voltage developed across the circuit is relatively low; maximum current will then flow in a load resistor, RL, in series with the circuit.
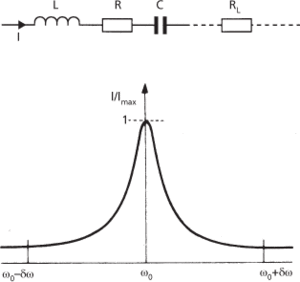
(a) Series resonant circuit and frequency response
In the case of a parallel resonant circuit, in which the circuit elements are in parallel (Fig. b), it is convenient to consider the combined admittance, Y, of the circuit (Y = Z−1), given by
The resonance condition is fulfilled when
i.e. when
Since the term R2C/L is usually very small this approximates to
which is the value of the series resonant frequency; the term however cannot always be neglected.
In a parallel resonant circuit therefore resonance occurs when the combined admittance is low. At resonance Z = 1/Y is high and is termed the parallel resistance of the circuit. The overall current is low but the voltage developed across the circuit, and therefore across a load resistor, RL, in parallel with it, is high. The individual currents developed in the inductance and capacitance at resonance can be very large but are out of phase with each other, resulting in the low combined current.
The above consideration leads to a unique solution for the resonant frequency. The resonant frequency may also be defined as that frequency at which the complex impedance passes through a minimum (in a series resonant circuit) or a maximum (parallel resonant circuit). In the series resonant case the solution is the same as above but in the case of parallel resonance a unique value is not necessarily found. The resonant frequency may have slightly different values that depend on the particular circuit parameter that is varied in order to achieve resonance. The differentials of Y with respect to C, L, or ω may therefore lead to slightly different resonance conditions.
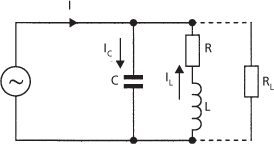
(b) Parallel resonant circuit
- biogenic
- biogenic amine
- biogenic deposit
- biogeochemical cycle
- biogeochemical exploration
- biogeochemistry
- biogeocoenosis
- biogeographic realm
- biogeography
- biogeomorphology
- bioglyph
- biographical approach
- bioherm
- biohistory
- biohorizon
- bioimmuration
- Bioinformatics
- bioinformatics
- bioinorganic chemistry
- biointermediate elements
- biolimiting elements
- biolistics
- biolithite
- biological agent
- biological clock