An example of a continuous-time Markov chain (see Markov process). The properties of queues are much studied by analysts of stochastic processes. Three components of a queuing system are the inter-arrival times (a Markov process (M), a more general process (G), or a pre-determined process (D), the service times (also Markovian, general, or predetermined), and the number of servers (k). The standard nomenclature for queues describes them as M/M/1, M/D/1, M/G/1, or G/M/k queues as appropriate.
The basic quantities of interest are the expected values of the number in the queue, the number waiting (i.e. not being served) in the queue, the queueing time, and the waiting time (the sum of the queueing and service times).
For an M/G/1 queue, with arrival rate λ and with 1/μ and σ2 denoting the mean and variance of the service time distribution and with ρ=λ/μ, then the expected value of the number in the system (queueing or being served) is N given by the Pollaczek–Khintchine formula
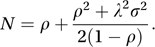
A useful general result, with t¯ denoting the average time spent in the system, is Little’s formula which states that λt¯=N.
1. (FIFO list, pushup stack, pushup list) A linear list where all insertions are made at one end of the list and all removals and accesses at the other. Like a pushdown stack, a queue can be implemented in hardware as a specialized form of addressless memory, and is most commonly used for speed buffering between a real-time data input/output stream and a form of memory that requires start/stop time.
2. See queue management, queuing theory.
A number of customers for a good or service waiting to be served. Queue discipline describes the order in which customers are served: this may be first-come first-served, random order, or last-in first-out, or some system of priorities may be used. Queuing models analyse the behaviour of queues, often using numerical simulation, and explore efficient ways of handling queues.
- one-to-one function
- one-to-one onto function
- O-network
- one-way filter
- one-way function
- one-way light time
- one-way linked list
- one-way travel time
- one-way valve
- one‐sided surface
- one‐sided test
- one‐tailed test
- one‐to‐many
- one‐to‐one
- one‐to‐one correspondence
- one’s complement
- one’s-complement notation
- onion weathering
- onium ion
- Onizuka, Ellison Shoji (1946–86)
- onlap
- online
- online analytical processing
- online auction
- online broker