The amount of information that a sample provides about the value of an unknown parameter. Writing L as the likelihood for n observations from a distribution with parameter θ, Sir Ronald Fisher in 1922 defined the information, I(θ), as being given by
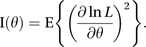 If T is an unbiased estimator of θ then a lower bound to the variance of T is
If T is an unbiased estimator of θ then a lower bound to the variance of T is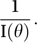 Since 1948 this has generally been referred to as the Cramér–Rao lower bound in recognition of the independent proofs by Cramér and Rao. The inequality Var(T)≥1/I(θ) (where ‘Var’ denotes variance) is the Cramér–Rao inequality.
Since 1948 this has generally been referred to as the Cramér–Rao lower bound in recognition of the independent proofs by Cramér and Rao. The inequality Var(T)≥1/I(θ) (where ‘Var’ denotes variance) is the Cramér–Rao inequality.If the distribution involves several parameters, θ1, θ2,⋯, θp, then the Fisher information matrix has elements given by
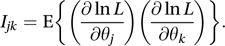
- lattice network
- lattice square
- lattice sum
- lattice vibrations
- latus rectum
- Latvia
- La Tène
- Laud, William (1573–1645)
- Laue, Max Theodor Felix von (1879–1960)
- Laue, Max von
- laughing gas
- Laughlin, Robert B.
- laughter
- laumontite
- launch
- launch and early orbit phase
- launch azimuth
- launch control centre
- launch/entry suit
- launch escape system
- launch pad
- launch phase
- launch processing system
- launch site
- launch umbilical tower