The problem of determining the distance from a starting position made by a walker, who can either move forward (toward+x) or backwards (toward −x) with the choice being made randomly (e.g. by tossing a coin). The progress of the walker is characterized by the net distance DN travelled in N steps. After N steps the root-mean-square value Drms, which is the average distance away from the starting position, is given by Drms=√N. Physical applications of the random walk include diffusion and the related problem of Brownian motion as well as problems involving the structures of polymers and disordered solids.
With the integers positioned as they occur on the real line, imagine an object moving from integer to integer a step at a time. The position Xn of the object at the nth step is part of a Markov chain X1, X2, X3,…, with state space being the integers. Such a Markov chain is called a one-dimensional random walk if Xn = i, then Xn+1 = i −1, i or i + 1, so that the object may stay where it is, or move one to the left or right.
When a gambler, playing a sequence of games, either wins or loses a fixed amount in each game, their winnings give an example of a random walk, with 0 being an absorbing state.
Random walks in two or more dimensions can be defined similarly.
See Brownian motion.
A walk in which the walker's movements are a consequence of a sequence of observations on one or more random variables. For example, suppose that, at each time point an individual walks one step to the left (with probability p) or one step to the right (with probability 1−p). This simple Markov process is a one-dimensional random walk. If the individual is allowed at each stage to move one step in any direction in two dimensions, then this is the drunkard's walk. The phrase ‘random walk’ was first used by Karl Pearson in 1905. See also Brownian motion.
In the particular case where p=0.5, it might be supposed that the proportion of time spent to the left of the starting point is likely to be close to a half. In fact the proportion is more likely to be near to 0 or 1. The probability of the time proportion being less than α (0≤α≤1) is given by the approximate arc-sine law:
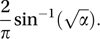
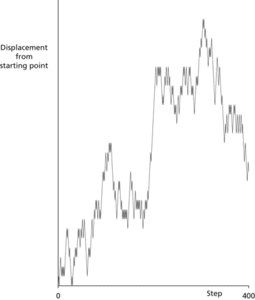
Random walk. The diagram shows the displacement from the starting point for the first 400 steps of a random walk in which each step has the same length, and moves up and down are equally likely. The x-axis represents the step number. The path is typical, in that it predominantly lies on one side of the starting line.
The problem of determining the distance from a starting position made by a walker, who can either move forward (toward +x) or backwards (toward –x) with the choice being made randomly (e.g. by tossing a coin). The progress of the walker is characterized by the net distance DN travelled in N steps. After N steps the root mean square value Drms, which is the average distance away from the starting position, is given by Drms = √N. Physical applications of the random walk include diffusion and the related problem of Brownian motion as well as problems involving the structures of polymers and disordered solids.
A stochastic process described by equation yt = yt−1 + εt where εt is white noise. It is a prototypical example of unit root process. Frequently considered versions are the random walk with drift, yt = yt−1 + δ + εt, and the random walk with drift and trend, yt = yt−1 + δ + γt + εt.
- grid base
- grid bias
- grid computing
- grid emission
- grid leak
- grid reference
- grid stopper
- grid zone
- Griesbachian
- Griess test
- Griffin, Donald Redfield
- Griffith, Arthur (1872–1922)
- Griffith cracks
- Griffith failure criterion
- Griffith, Fred
- Griffith–Murrell failure criterion
- griffon vulture
- Griggs, (Stanley) David (1939–89)
- Grigg–Skjellerup
- Grigg–Skjellerup, Comet 26P/
- Grignard, François Auguste Victor
- Grignard reagents
- grike
- Grimaldi, Francesco Maria
- Grimm–Sommerfeld rule