See circular measure.
In elementary work, angles are measured in degrees. In more advanced work, particularly involving calculus, it is essential that angles are measured in radians. For example the differential of sine is cosine only when radians are used.
Suppose that a circle of radius 1 with centre O meets two half-lines from O to A and B. Then the size of ∠AOB, measured in radians, equals the length of the arc AB.
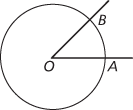
On a unit circle, the arc AB equals ∠AOB in radians
1 radian is approximately 57°. More accurately, 1 radian≈57.296°≈57° 17′45″. Since the circumference of a unit circle is 2π, one revolution or 360° measures 2π radians. Consequently, x° = πx/180 radians.
The radian is the SI unit for measuring angle.
Compare steradian.
A unit of angle used in geometry. It is defined as the angle subtended at the centre of a circle by an arc of equal length to the radius of the circle. The whole circumference of the circle, of length 2π times the radius, subtends an angle of 2π radians; thus, 360° = 2π radians, and 1 radian = 57°.2958. A useful approximation for astronomers is that 1 radian is about 200 000 seconds of arc (actually 206 265). As a consequence of the definitions of the units, the number of seconds of arc in a radian equals the number of astronomical units in a parsec.
A unit of angle measurement. The radian measure of the angle enclosed between two lines OP and OQ is defined to be the length of the circular arc, with centre O and unit radius, enclosed between the lines. Thus a right angle is π rad, and a complete revolution corresponds to 2π rad. The relationship with degrees is that π rad=180° or 1 rad≈57.296°. Use of radians is important when trigonometrical functions are used in calculus. For example, in the relationship that the derivative of sin x is cos x.
The plane angle between two radii of a circle that form an arc on the circumference that is equal in length to the radius.
A unit of measurement for angles; one radian corresponds to the angle whose arc length on a unit circuit is itself 1. A single radian equals approximately 57.3 degrees and full rotation corresponds to 2π radians. It is the natural unit for angles, and the one required for the simplest forms of trigonometric equations to hold.
- extravehicular activity
- extremely high frequency
- Extremely Large Telescope
- extreme Population I star
- extreme ultraviolet
- Extreme Ultraviolet Explorer
- Extreme-Ultraviolet Explorer
- extreme value distribution
- extreme-value distribution
- extremophile
- extremum
- extrinsic
- extrinsic photoconductivity
- extrinsic properties
- extrinsic semiconductor
- extrinsic value
- extrinsic variable
- extrusion
- extrusion reaction
- extrusive
- exurb
- eye
- eye candy
- eye lens
- eyelet-construction mica capacitor