For the discrete random variable X, with probability distribution P(X=x_j), j=1, 2, 3,…, the probability-generating function G is defined by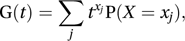where t is an arbitrary variable. Note that G(t) is the expected value of t^X and G(1)=1. If the set of possible values of x is infinite, |t| needs to be small enough for the series to converge.

If the first and second derivatives of G(t) with respect to t are denoted by G′(t) and G″(t), respectively, the expected value and variance of X are given by G′(1) and G″(1)+G′(1)−{G′(1)}², where, for example, G′(1) denotes the value of G′(t) when t=1.

Like the moment-generating function, the probability-generating function can provide a useful alternative description of a probability distribution. For example, if Y denotes the sum of n independent random variables, each having pgf G(t), then P(Y=y) is the coefficient of t^y in {G(t)}ⁿ.

Another useful property is that, if X and Y are independent random variables with probability-generating functions G_X(t) and G_Y(t), respectively, then the probability-generating function of Z=X+Y is G_Z(t), where

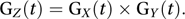
De Moivre used the probability-generating function technique in 1730. The term itself became common following its use by Bartlett in 1940. See also moment-generating function.