For a continuous random variable X, a probability density function (or pdf) of X is the function fX such that
A probability density function is necessarily non-negative with integral 1. The Cantor distribution is an example of a continuous random variable which does not have a probability density function.
Suppose that, for the random variable X, a sample is taken and a corresponding histogram is drawn with class intervals of a certain width. Then, loosely speaking, as the number of observations increases and the width of the class intervals decreases, the histogram assumes more closely the shape of the graph of the probability density function.
For a continuous random variable X the probability density function f is such that
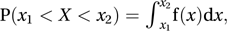 for all x1<x2. Because, for a continuous random variable, P(X=xj)=0 for any value xj, either or both of the ‘<’ signs in the left-hand side can be replaced with ‘≤’. If the interval of possible values for X is (a, b), then
for all x1<x2. Because, for a continuous random variable, P(X=xj)=0 for any value xj, either or both of the ‘<’ signs in the left-hand side can be replaced with ‘≤’. If the interval of possible values for X is (a, b), then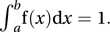 It is often convenient to regard the function f as being defined for all real values of x. This can be achieved by taking f(x)=0 for x outside the interval (a, b), so that
It is often convenient to regard the function f as being defined for all real values of x. This can be achieved by taking f(x)=0 for x outside the interval (a, b), so that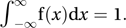 This property, and the property that f(x)≥0 for all x, are essential properties of a probability density function. It should be noted that, although f(x) is related to probability, f(x) can exceed 1.
This property, and the property that f(x)≥0 for all x, are essential properties of a probability density function. It should be noted that, although f(x) is related to probability, f(x) can exceed 1.The probability density function is often referred to simply as the probability density. It is related to the cumulative distribution function F by
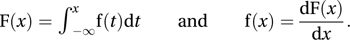 The probability density function is not necessarily continuous. At a point of discontinuity the value assigned to f(x) is immaterial.
The probability density function is not necessarily continuous. At a point of discontinuity the value assigned to f(x) is immaterial.
In statistics, the mathematical function which allocates probabilities of particular observations occurring. The probability density function may be used to construct a frequency distribution of certain events occurring either discretely, in the form of a histogram, or continuously.
- synrhabdosome
- synroc
- synrock
- synsacrum
- synsedimentary fault
- synsedimentary fold
- syntactic consequence
- syntactic engine
- syntactic error
- syntactic monoid
- syntax
- syntax analyser
- syntax analysis
- syntax diagram
- syntax error
- syntaxial growth
- syntaxin
- syntax tree
- syntectonic
- synteny
- syntexis
- synthem
- synthesis
- synthesis gas
- synthesizer