An expansion, derived by Edgeworth in 1905, that relates the probability density function, f, of a random variable, X, having expected value 0 and variance 1, to φ, the probability density function of a standard normal distribution, using the Chebyshev–Hermite polynomials. The first terms of the expansion are 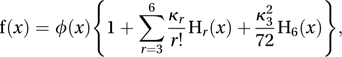where κ_r is the rth cumulant of X, and H_r(x) is the rth Chebyshev–Hermite polynomial. See also Cornish–Fisher expansion.