Description of a situation where events occur randomly in time, or space, in such a way that for each small interval of time, or small region of space, the probability that it contains exactly one event is proportional to the size of the interval or region. It is assumed that this probability is independent of whether or not any other small intervals, or regions, contain an event, and it is also assumed that the probability of two events occurring in the same small interval or region is 0. This is a mathematical description of randomness. As the diagram overleaf shows, randomness usually gives rise to apparent clustering, despite the natural expectation that randomness would lead to regularity.

For events that occur at random instants in time, the formal defining properties of a Poisson process arewhere k is a positive constant. The number of events in a time interval of length t has a Poisson distribution with parameter kt.

The time intervals between events, and from the start of observations to the first event, have independent exponential distributions with parameter k, mean 1/k, and variance 1/k². The time interval from the start of observations to the nth event has an Erlang distribution (see gamma distribution) with probability density function f given by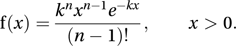The mean of this distribution is n/k and the variance is n/k².

An example of a naturally occurring Poisson process is the emission of α-particles from a radioactive source. A compound Poisson process is a process in which the events of interest occur in ‘packets’ (e.g. buses) that arrive randomly at a steady rate. The number in each packet is an observation from the same distribution (e.g. a uniform distribution between zero and the capacity of a bus).

Poisson process. The diagram shows 200 points, randomly scattered such that each location was equally likely; the points were generated using pseudo-random numbers. The arrangement shows the typical characteristics of a spatial Poisson process with apparent clumps and blank spaces.