A type of digital signal processor that performs the actions of an electrical filter but on sequences of discrete sampled data as the input signal rather than a continuous signal as in the case of an analogue filter (see diagram). The ADC (analogue-to-digital converter) performs the task of converting the continuous signal x(t) into discrete samples. The digital filter processes the digital sequence to perform the required filter response, and the resulting digital output is converted back to a continuous signal y(t) by the action of the DAC (digital-to-analogue converter).

The digital filtering process can be achieved in either the frequency domain or the time domain. The frequency domain analysis involves a transformation of the discrete signal into its corresponding spectrum, possibly by the use of a DFT or FFT algorithm (see discrete Fourier transform). The resulting frequency components are adjusted in accordance with the desired filter characteristic.

In the time domain, which is the most common form of digital filtering, the discrete signal samples are acted upon directly to produce the desired filtering characteristic. There are two methods that can be adopted to obtain the filter characteristic. One method, known as finite impulse response (FIR), involves the summation of input samples x(n) with the delayed samples of the input x(n–1) scaled by the filter coefficient (which is also known as the tap weight); this results in FIR filters (also known as nonrecursive filters or transversal filters). Alternatively, a summation of the input samples x(n) with delayed values of the output signal y(n–1) results in filters known as infinite impulse response (IIR) filters (or recursive filters).

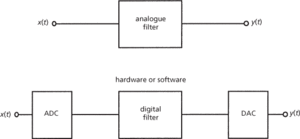
Digital filter compared with analogue filter