For the real function f, if (f (a + h)−f (a))/h has a limit as h → 0, this limit is the derivative of f at a and is denoted by f ′(a). (The term ‘derivative’ may also be used loosely for the derived function.)

Consider the graph y = f(x). If (x, y) are the coordinates of a general point P on the graph, and (x + Δ‎x, y + Δ‎y) are those of a nearby point Q on the graph, the quotient Δ‎y/Δ‎x is the gradient of the chord PQ. Also, Δ‎y = f(x + Δ‎x)−f(x). So the derivative of f at x is the limit of the quotient Δ‎y/Δ‎x as Δ‎x → 0. This limit can be denoted by dy/dx, which is thus an alternative notation for f ′(x). The notation y′ is also used.

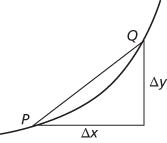
PQ’s gradient approximating the curve’s

The derivative f ′(a) gives the gradient of the curve y = f(x), and hence the gradient of the tangent to the curve, at (a,f(a)). If x is a function of t, where t denotes time, then the derivative dx/dt is referred to as a rate of change and may be denoted by $\dot{x}$. The modulus function f(x) = |x| is an example of a function which does not have a well-defined derivative at x = 0 (see also blancmange function). For the derivatives of certain common functions, see appendix 7. See also differentiation, higher derivative, left and right derivative, partial derivative.