【家电产品质量分级中的模糊数学概念】
拼译:appllcation of fuzzy mathematics to the quality appraisal of housekeeping electrical appliances
现代数学与集合论密切相关,集合可以表现概念,集合的运算和变换可以表现判断和推理。在普通集合论中,一个元素对于一个集合,要么属于、要么不属于,二者必居其一,且仅居其一。这样就限定了普通集合论只能表现“非此即彼”的现象。当代许多学科的分类标准和等级指标反映了普通集合论的这个特征。如目前的洗衣机产品质量分级规定,就是这种“非此即彼”的二值逻辑的体现。在产品质量分级的限定值(区间)制定后,某产品的检测值对该等级而言,就成了要么属该等级,要么不属该等级.这样的级别划分方法,在级与级的分界处形成了一个突变,表现不出级别之间的自然过渡及同一级别内的性能差异。事实上产品的性能是顺序渐变的,而现行的产品质量分级的规定,却将顺序逐变的过程在某些限定值处,人为地断开,形成一个级别的突变。因此,要使考核项目的级别划分更接近人们的自然感觉和判断,就必须接受这样一个事实:即不同的级别之间存在着一个中介过渡状态,级别间的过渡是一个顺序渐变的过程;级别内也存在对该级别的符合程度上的差异。要描述这样的具有“亦此亦彼”的模糊概念,就要借助于“模糊集合论”的有关理论。1965年,美国L.A.Zadeh根据工作中的体会写出了一篇名为《模糊集合》的论文,开始用数学的观点刻划事物的模糊性。
若以洗衣机产品质量的分级为例,现行的《家用洗衣机产品质量分级规定(草案)》中的解释“C级:产品一般水平”。而产品的一般水平显然是一个模糊概念,其外延是极不分明的。为此,特构造如F的模糊统计试验:通过调查,对洗衣机噪声的“一般水平”,根据各自的体验和理解,确定一个噪声的取值范围,即给出ζ和η的一对数值,ζ:C与B级的分界点;η:C与D级的分界点。只要找出了ζ和η的概率分析,就可确定C级的隶属函数表达式。对于这样的三相模糊统计试验,有如下的定理。定理:设(ζ,η)是满足P(ζ≤η)=1的连续随机变量,对于(ζ,η)的每一次取值,都联系着一个映射: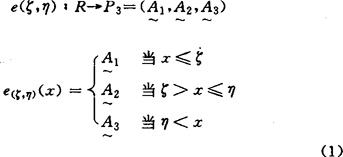
则由此三相模糊统计试验所确定的三相隶属函数为:
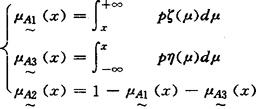
式中Pξ(μ)和Pη(μ)分别分别为ζ和η的边缘概率密度函数。
由于(ζ,η)是被调查者在大量的独立作用的各种因素综合影响下所做出的选择,考虑到人们在认识上有趋于一致性的正态分布特点,可导出上述定理的推论如下:推论:设ζ:N(α1,σ2),η:N(α2,σ2)则三相模糊统计所确定的三相隶属函数(式2),可简化为: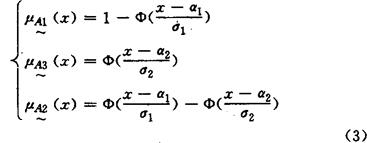
式中Φ(x)为正态分布的分布函数。
根据式3及噪声G级的限定值(C与B级的分界点为67dB;C与D级的分界点为71dB),并考虑到每个噪声测试值只可能对两个相邻级别产生隶属关系,可得出式4描述的C级隶属函数。同理,也可确定出噪声各个级别的隶属函数。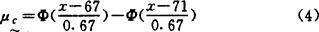
(北京轻工业学院乔五之教授撰)