【作物正态回归模型】
拼译:normal regressiion moldel of crop
又称指数二次多项式模型,它在描述作物的生长、发育与生态条件关系时,较直线、指数曲线、对数曲线、幂函数曲线、双曲线及二次曲线等回归模型更接近于实际。正态回归模型在作物产量分析、产量预测、作物区划、农业规划和作物生长发育的计算机模似等方面有广阔应用前景。
自18世纪40年代初Reaumur创立积温学说以来,人们一直在使用直线回归模型来描述作物生长发育与温度之间的关系,认为作物生长发育速度与气温呈直线正相关。其表达为1/N=(t-B)/A,式中1/N为发育速度,t为温度,4为有效积温,B为有效温度下限。人们很快发现,这种直线回归模型虽然在一定温度范围内是合理的,但就其整体来说是不符合生物学规律的。作物的发育速度不可能随着温度的无限升高而加快,也不能随着温度的无限下降而减慢,甚至变成负值。任何作物的生长和发育的速度都应有最大值和最小值,而且最小值为0。后来,人们先后使用了指数、对数、幂函数、双曲函数和抛物线模型Y=a+bx+cx2,当c<0时,是个有最大值的连续函数,这是对直线模型的改进,但它仍没有最小值。也有些学者用分段拼合的方法来描述作物的生长发育与气象条件的关系。比如,在某一段用近似于直线的正相关来描绘,在另一段用近似于直线的负相关描绘,这样虽然可使模型出现最大值,但在两段接合处,函数出现不连续点,其导数不存在,无法进行数学分析。同时,这种函数曲线的突然转折也是不符合生物学规律的。20世纪30年代,日本农业气象学者提出,用正态回归模型来描述作物生长发育与气象条件的关系可能更为合理。因为正态回归模型可以做到,当气象因子处于适当值时,使表示作物生长发育速度的函数达到一个极大值,而气象因子向低值或高值变化时,使函数趋于最小值0。但是由于当时计算技术的落后,未能投入实际使用。70年代初,苏联学者德米特连科(В.Л.Дмигpeнкo)开始将正态回归模型应用于描述作物产量与水文气象条件的关系,并初步解决了对称和不对称的问题。他所提出的正态回归模型的表达式为 m(T)=M(T0)EXF{-a[(t-t0)/10]2}式中,m(T)为温度等于T时的生产量,M(T0)为最适温度T0时的最大生产量,a为参数。若不对称时,当T≤T0时a=1,当T>T0时,a=2。1979年,法国马累特(Ph.Malet)指出,对作物生长曲线模型取一阶导数就可得出正态回归模型。1984年,弗朗斯,(J.France)和梭恩莱(J.H.M.Thornley)指出,用指数多项式可描述作物生长量与时间的关系,其中指数二次多项式正是一元正态回归模型。其表达式为:W=EXP(a0+a1t+a2t2)1984年,莫惠栋指出,生物在单位时间内的生长量或发生量是接近正态的,提出了Y=a EXP(bx2)形式的模型,这也是正态回归模型的特例,并指出正态累积函数是S型生长曲线。1987年,黑龙江省农垦科学院张隐君和李德明,在运用正态回归模型研究春小麦产量与气象条件的关系时,提了多元正态回归模型的表达式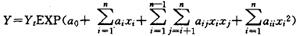
式中,a0为常数项,ai为一次项回归系数,aij为交互项回归系数,aii为平方项回归系数,Yt为产量趋势,Y为产量。同时还提出了标准正态回归模型和失真正态回归模型的概念,给出了标准正态模型的判别式。
1989年,吉林农业科学院丁希泉在其著作中指出,高梁、小麦、玉米和大豆等作物的灌浆速度与时间的关系,均呈正态回归曲线形式。还指出各种生长曲线,其中包括逻辑斯谛(Logistic)曲线,经变换都可变成正态回归曲线或类似正态回归曲线的形式。1989年黑龙江省农垦科学院将正态回归模型方法与气象数据库系统结合,在计算机上实现了对正态回归模型的因子筛选、建模、检验、解析、极值判别、最大值求算、确定取得最大值时的因子组合和绘制正态回归曲线或曲面图等工作的自动化。利用上述计算机系统,他们还分别对当地主栽作物与光、温、水等气象条件的关系进行了分析,建立了许多一元、二元和多元正态回归模型。并利用这一系统还对国内21个省的农业气候资料进行了分析,并与吉林省农业科学院潘铁夫等合作,以正态回归模型为基础,建立了中国大豆生长发育动态的计算机模型。1991年10月中国农学会农业气象研究会于南京召开作物计算机模似与作物气象学术讨论会,专家们一致同意成立作物计算机模拟协作组,其中大豆协作组以吉林和黑龙江等省的人员为核心。1992年,黑龙江省农垦科学院还将作物正态回归模型应用于模似气候变暖对作物生长发育的影响,得出了一些有益的结论,提出了几条可行的对策。正态回归模型有许多优点,但也有不足之处。主要是由于模型的外围是逐渐趋近于最小值的,这给确定适合作物生长发育所需环境因子的最低值和最高值带来了一定困难。当前,由于计算技术的迅速发展和作物正态回归模型理论的逐步形成,给模型应用开辟了更加广阔的前景。预计在20世纪内,正态回归模型研究和应用的主要热点是:(1)模型理论进一步完善的问题;(2)利用正态回归模型模似作物生长发育进程的问题;(3)进一步拓宽应用领域的问题;(4)解决不对称模型建模方法的问题。【参考文献】:1 西涅里西柯夫B B.农业气象预报和测报方法.北京:北京农业大学,1961,86~882 Дмитpeнко B H.作物气象生态译丛,北京:农业出版社,1984,111~1143 张隐君,等.黑龙江气象,19874 丁希泉,等.农业实用回归分析.(第10版).长春:吉林科学出版社,1989,7:333~3425 李德明.现代化农业,1989,116 李德明,等.第1届全国农业计算机应用技术交流研讨会论文集.北京:中国农业科学院计算中心,1990,12:284~2857 潘铁夫,等.中国农业气象,1993,14(4):1~88 莫惠栋.农业试验统计.上海科学出版社,1992,1:434~4399 史纪明,等.全国计算机农业应用技术学术交流会(第2届)论文集.北京:中国农业科学院计算中心,1992,44~4610 李德明,等.全国计算机农业应用技术学术交流会(第2届)论文集.北京:中国农业科学院计算中心,1992,229~231(黑龙江省农垦科学院李德明高级工程师、胡瑞瑶工程师撰)