【模糊误差理论与矿山测量模糊数据处理】
拼译：the fuzzy error theory and processing of fuzzy data in mine surveying
误差理论是1809年德国高斯(C．F．Gauss)创立的。他从概率论观点出发，提出了指数型分布函数，又称正态分布函数。高斯误差理论的创立为研究和处理偶然误差指出了正确方向，故沿用至今。但高斯误差理论的中心是它的误差分布函数，这是正态分布函数，这在现代的测量精度要求越来越高的条件下，测量中的系统误差就突出表现出来。
1928年，德国学者在导线测量中发现，只按偶然误差理论的“边长测量中误差随边长平方根增长”的论断是不能估算出边长误差的，为此，提出－个经验公式估算导线的纵向误差，其中除增加系统误差影响系数外，还增加一个常数项。这说明观测误差中同时存在偶然误差集合和系统误差集合，两种集合误差同时出现，两个集合将成为模糊误差集合。这个综合误差的分布函数，显然不是标准正态分布函数。后人出于维护高斯误差理论，又提出了两项措施：一是进行系统误差检验；二是采取措施剔除系统误差，以便仍用高斯误差理论处理数据。但系统误差影响因素众多，很难避免在观测成果中不存在系统误差。系统误差中并不是只含恒定系统误差，同时还含有可变系统误差。偶然误差集合和系统误差集合在误差论域里所占的比重模糊不清，很难区分，从而构成了误差的模棱两可性和复杂性，因而产生误差集合划分上的不确定性，乃至导致测量误差的模糊性，在此基础上研究和提出了模糊误差理论问题，首先是模糊偶然误差集合和模糊系统误差集合问题。误差划分上的不确定性必然造成误差元素对某一集合隶属关系的不确定性。1965年，美国L．A．Zade提出了模糊子集论，提出隶属资格概念，认为要确定一个模糊子集，只要确定其隶属资格或隶属函数。并根据这一理论确立了模糊误差子集的表示方法，还分别建立了模糊偶然误差集合Ã和模糊系统误差集合B的隶属函数，记UA(∑)和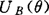
，其值分别表示误差元素ε和θ隶属于A和B的隶属资格，隶属资格
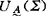和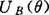
之值越接近于1，表示误差A和B属于模糊偶然误差集合Ã和模糊系统误差集合B的资格程度越高，出现可能性越大。陶华学参加的“模糊误差理论研究和矿山测量模糊数据处理”研究，提出了模糊误差子集的表示方法和运算方法，模糊误差集合及子集的隶属函数的理论求法及其函数式以及它的特性。研究表明，模糊误差全集合的隶属函数曲线形态属偏态分布，模糊偶然误差集合的隶属函数曲线形态属正态分布，它除了具有普通误差集合的特性外，还具有以下3个特性：第一，隶属资格的对称性；第二，绝对值小的模糊偶然误差隶属属于Ã的资格大，而绝对值大的模糊偶然误差隶于A的资格小；第三，绝对值很大的模糊偶然误差隶属于Ã的资格接近于零，即有界性。模糊系统误差集合的隶属函数曲线形态属均匀分布。从有关资料分析得知，均匀分布的数学期望正好是系统误差集合内各误差元素分布的中点。它具有以下两个特性：第一，在闭区间内的系统误差均有相等的隶属资格；第二，正确度b即是模糊偶然误差集A的分布中心，又是模糊系统误差集合B的中点，经典误差域中误差计算已有固定方法，而模糊误差集Ã和B之间的误差计算已不是一般计算，而是误差合成，为此应用凸模糊集，以模糊数和模糊数的运算方法导出模糊误差集的误差合成规律，两个模糊误差集合之间的合成关系就是模糊数之间的计算问题。根据模糊误差集的误差合成规律，可以研究各类测量工作中测量误差的影响规律和分列出系统误差的影响规律和偶然误差的影响规律，还可以对模糊偶然误差和模糊系统误差进行合成计算，从而可客观、合理地探讨误差集合领域内误差的累积规律。为了判定两个模糊误差集合之间的贴近程度，定义了模糊权，导出了模糊权的计算式，包括同类观测值集合的模糊权计算和非同类观测值模糊权计算。经典误差理论中常用的权，一般只能用于计算均值和离散误差，而不能鉴定观测成果的真正“可靠程度”。根据模糊集合的贴近度定义的模糊权，可鉴定它的“可靠程度”，另外从模糊权计算式中可看出，谁最贴近样本集合，谁的权最高，它的“可靠程度”也最高。应用模糊集合原理进行矿山测量中的模糊数据处理，一般有以下几方面：(1)用模糊集合原理优选矿山控制网布网方案。可能有的布网方案为评判对象集合，优选方案同时考虑精度U1、可靠性U2和经济U33个指标，称为评判指标因素集合U。还可将这一指标因素划分层次得第2级因素，称为第2评判集合。总评语取优、一般、差。根据评判因素特点构成各因素评价模型，再根据评判顺序先对U1进行单因素评判。为此，需通过比较U1中各因素间相对重要性给出权重向量，求得U1各因素对评语的隶属度，构成评判矩阵可得U1中各因素对评语的评判结果。考虑U2、U3各因素进行综合评判，可找出最优布网方案。(2)根据模糊集原理评定矿山测量图纸质量，主要依据绝大多数是具有模糊性的因素，为此，需采用模糊综合评判法评定矿图质量。主要依据包括：图中各要素选取与概括的合理程度，图中各要素之间关系处理适应程度，矿图精度，矿图空间关系现势性程度，矿图表示上的错漏，线划工艺质量，注记的正确、合理程度。对上述7个方面组成论域U，评定矿图质量的评语为“优、良、中、差”4个级别，对论域U中各元素值可依据它们的隶属函数确定组成模糊距阵R，求得模糊向量Ã。向量Ã中元素值为上述7个因素的权数，这些权数可由难易程度、强调的方面等而定。对该矿图质量进行评定，可得出该矿图质量应属的等级。(3)根据模糊聚类分析进行矿山地表沉降变形观测分析，沉降变形观测的聚类分析按下述几步进行：第一，求得沉降变形模糊关系矩阵；第二，由标定得到的模糊矩阵是一个模糊相似矩阵，但不一定能满足传递性，因此需要由模糊相似矩阵构造一个新的模糊等价矩阵；第三，进行动态聚类分析；第四，用Kruskal最大树法确定下沉点。此外，还可应用模糊综合评判方法对观测成果质量进行综合评判；应用模糊识别方法对三角网中的三角形、多边形识别，对经纬仪导线的模糊识别等。模糊误差理论的研究和矿山测量模糊数据处理的应用还是局部的，今后将进一步拓宽、完善，运用于各测量领域。【参考文献】：1 汪培庄．模糊集合论及其应用．上海：上海科学出版社，19832 徐忠．测绘通报，1984，63 Tao Huaoxue，ISM．1988，74 陶华学．矿山测量，1989，25 陶华学，等．中国煤炭科学基金科研成果论文集．北京：煤炭工业出版社，1992(山东矿业学院博士生导师陶华学教授撰)