Any statistic of the form
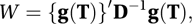 where T is an estimator of a vector parameter θ, g is some vector-valued function, and D is an estimator of the variance–covariance matrix of the vector {g(T) − g(θ)}. The statistics are used to test the null hypothesis that g(θ)=0, where 0 is a vector with all entries equal to 0. If T is the maximum likelihood estimator then W has an approximate chi-squared distribution with p degrees of freedom (where p is the number of elements in θ).
where T is an estimator of a vector parameter θ, g is some vector-valued function, and D is an estimator of the variance–covariance matrix of the vector {g(T) − g(θ)}. The statistics are used to test the null hypothesis that g(θ)=0, where 0 is a vector with all entries equal to 0. If T is the maximum likelihood estimator then W has an approximate chi-squared distribution with p degrees of freedom (where p is the number of elements in θ).
- read-write head
- read/write head
- read-write memory
- read/write memory
- ready signal
- Reaganomics
- Reagan, Ronald (1911–2004)
- reagent
- real
- real-aperture radar
- real axis
- real balance effect
- real balances
- real business cycle
- real component
- real costs
- real definition
- real effective exchange rate
- real essence
- real exchange rate
- real function
- realgar
- real gas
- real GDP
- real GNP