In fluid dynamics, the equation
which is a consequence of conservation of mass. Here ρ denotes density and u is the fluid’s velocity. Consequently, if the fluid is incompressible and ρ is constant, then divu = 0. The term is more generally used for similar equations that arise in applied mathematics as a consequence of a quantity being conserved.
An equation that describes the total transport of a conserved quantity moving from one place to another within a pipe, process, or system. It applies to the transport of mass, energy, momentum, and all other natural quantities. Expressed as a simple balance equation, the transport into a system is equal to the transport leaving. There is neither accumulation nor depletion within the system under steady conditions. The conserved quantity is usually defined with reference to a flow area.
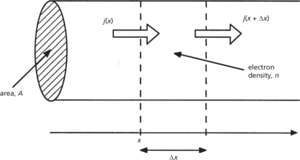
An equation that relates the time rate of change in the number of particles in a given volume to the inflow and outflow of particles. In electronics, this usually refers to the continuity of electrons or holes in a semiconductor in which current is flowing. When considering the flow of electrons in a piece of semiconductor, the electron continuity can be determined by considering the flow of electrons through an elemental slice of the semiconductor (see diagram). The rate of change of the number of electrons in the elemental volume of width Δx is equal to the number of electrons flowing in minus the number flowing out, plus the number generated per unit time minus the number that recombine (with holes) per unit time:
where N is the number of electrons. Considering the diagram, this can be written as
where n, the number density of electrons, is multiplied by the elemental volume (A.Δx) to obtain the actual number; j(x) is the flux of electrons across the plane at x, and G and R are generation and recombination rates of electrons per unit volume, respectively.
If the width of the element, Δx, is small enough, then using the definition of differentiation:
the flow terms in j can be replaced, yielding a continuity equation:
Normally in electronics, the flux term is expressed as a current density, J, which can be measured. Thermal generation and recombination are processes that are continually occurring in a semiconductor, and are balanced in equilibrium. It is more usual to consider the recombination of excess charge carriers in a semiconductor, or how the carriers in the semiconductor progress from nonequilibrium conditions back to thermal equilibrium. Thus, cancelling the thermal components from G and R, and substituting for current density,
which for electrons can be written
The first term is derived from drift current, where μ is the electron drift mobility and E is the electric field; the second term is derived from diffusion current, where D is the electron diffusivity; n0 is the equilibrium electron density and 1/τ is the recombination rate for electrons. A similar expression can be written for holes.
Continuity equation: particle flow
All landscapes must obey an equation for the conservation of mass: mass, energy, or momentum are conserved in a system, so that for any part of the system the net increase in storage is equal to the excess of inflow over outflow of the quantity conserved. In rectangular coordinates and in differential form, the continuity equation is:
where ρ is fluid density and u, v, and w are velocity components in the x, y, and z directions. Geomorphologists apply this equation to all cases of mass balance. Applied to mass transactions on a hillslope, the continuity equation states that if more material enters a slope section than leaves it, then the difference must be represented by aggradation; conversely, if less material enters than leaves, then the difference must represent net erosion. The same principle of continuity of sediment transport applies to other geomorphic systems including rivers; see Dietrich and Perron, 2006 Nature 439, 411.
- Ludfordian
- Ludhamian
- Ludlow
- Lu, Edward Tsang (1963)
- lugworm
- Luhn algorithm
- Luisian
- Lukács, György (1885–1971)
- Lull, Ramon (c.1232–1316)
- lumbar vertebra
- lumbar vertebrae
- lumen
- luminance
- luminance flicker
- luminescence
- Luminescence Dating
- luminol test
- luminosity
- luminosity class
- luminosity density
- luminosity evolution
- luminosity function
- luminosity–volume test
- luminous arc
- luminous blue variable