For a random variable X the rth moment (about the origin) is defined to be the expected value of X^r, where r is a non-negative integer. It is usually denoted by μ′_r. So μ′₀=1 and μ′₁=μ, the mean of X.

The rth moment about the mean (or central moment or corrected moment) is defined to be the expected value of (X−μ)^r and is usually denoted by μ_r. Thus μ₁=0 and μ₂=σ², the variance of X. The moments about the mean can be expressed as linear combinations of the uncorrected moments, for example: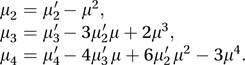Either set of moments can also be expressed in terms of linear combinations of simple functions of the cumulants. It should be noted that, for some distributions, μ_r′ and μ_r may exist only for small values of r.