“mode”的概念、定义、翻译、参考文献-科学参考

mode

Physics

1. The pattern of motion in a vibrating body. If the body has several component particles, such as a molecule consisting of several atoms, the modes of vibration are the different types of molecular vibrations possible. In the case of a vibrating string, the different modes of vibration of the system are characterized by the number of nodes in the string (see harmonic).

2. The number that occurs most frequently in a set of numbers. For example, the mode (modal value) of {7, 6, 2, 1, 2, 1, 2, 4} is 2. If a continuous random variable has probability density function f(x), the mode is the value of x for which f(x) is a maximum. If such a variable has a frequency curve that is approximately symmetrical and has only one mode, then (mean−mode)=3(mean−median).

Mathematics

The most frequently occurring observation in a sample or, for grouped data, the group with the highest frequency. For a continuous random variable, a value at which the probability density function has a global maximum is called a mode.

Statistics

A data value, in a set of categorical data, whose frequency is not less than that of any other data value. For a set of numerical data, a mode is a data value whose frequency is not less than the frequency of neighbouring values. If the numerical data is in the form of grouped data, a modal class is a class whose frequency is not less than the frequency in neighbouring classes. The modal frequency is the frequency with which the mode occurs, or the frequency in the modal class.
For example, the time intervals (in minutes, to the nearest minute) between the eruptions of Old Faithful on 1 August 1978 were $mode$
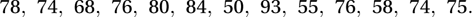
The values 74 and 76 both occur twice, and the remaining values occur just once. The values 74 and 76 are the two modes, both having a modal frequency of 2. Combining the data from 1–8 August, we have the following summary table:
Time interval
40–49
50–59
60–69
70–79
80–89
90–99
Frequency
5
21
10
37
30
4
The modal classes are 50–59 (with modal frequency 21) and 70–79 (with modal frequency 37).
For a discrete random variable a mode is a value whose probability is not less than that of its neighbours. For a continuous random variable a mode is a value such that the probability density function has a local maximum. If there is only one mode the distribution is unimodal. If there is more than one mode the distribution is multimodal. If there are two modes it is bimodal. The word ‘mode’ was coined by Karl Pearson in 1895.
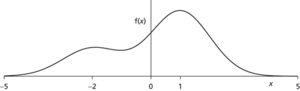
Mode. The multimodal probability density function illustrated is for a mixture distribution of two normal distributions, each with unit variance. One is centred on x=1 and the other on x=−2.

Chemistry

The pattern of motion in a vibrating body. If the body has several component particles, such as a molecule consisting of several atoms, the modes of vibration are the different types of molecular vibrations possible.

Chemical Engineering

1. A type of statistical average. In a discrete set of data, it is a single value. If the data is continuous, the mode is the point of greatest clustering of occurrences. It is used when the most typical value is required.

2. A type of operation of a controller used to control a process that can either be manual, automatic, or remote. In automatic mode, the controller calculates the output value as the difference between the set point and the measured process variable. In manual mode, the process operator sets the output, while in remote control, the controller obtains the set point from another controller.

Computer

1. A term used in many contexts concerning the operation and use of a computer system. For example: conversational mode refers to interactive computer use; interpretive mode refers to a way of executing a language; there are addressing modes in instruction descriptions.
2. See measures of location.

Electronics and Electrical Engineering

1. (transmission mode) Any one of the several different states of oscillation of an electromagnetic wave of given frequency. The mode of an electromagnetic wave depends upon the configurations of the vectors describing the wave; three main types of wave exist:
- • TE waves (or H waves) are transverse electric waves in which the electric field vector (E-vector) is always perpendicular to the direction of propagation, z, i.e.
  $E_{z} = 0$
- • TM waves (or E waves) are transverse magnetic waves in which the magnetic vector (H-vector) is always perpendicular to the direction of propagation, z, i.e.
  $H_{z} = 0$
- • TEM waves are transverse electromagnetic waves in which both the E-vector and the H-vector are perpendicular to the direction of propagation, i.e.
  $E_{z} = H_{z} = 0$
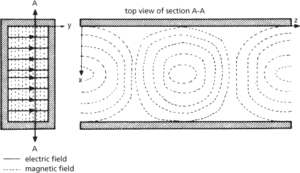
(a) Field configuration for TE_1,0 wave in rectangular waveguide
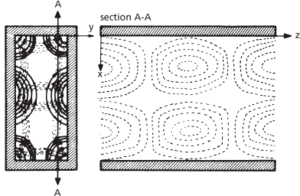
(b) Field configuration for TE_2,1 wave in rectangular waveguide
The TEM mode is the one most commonly excited in coaxial lines. It cannot be propagated in a waveguide.
Solving Maxwell’s equations for the particular conditions existing, it is commonly found that the solutions are characterized by the presence of one or more integers (m, n) that can take values from zero to infinity; this allows several possible modes for each type of wave. The physical constraints and the frequency of the radiation usually limit the number of permitted values of m and n and therefore the number of possible modes.
A particular example may be considered. In a waveguide each component of the wave contains a factor given by
$exp (jω t - γ_{m, n} z)$
where ω is 2π times the frequency and j is √−1; γ_m,n is the propagation coefficient and determines the phase and amplitude of the wave components. For each mode a lower limit exists where the complex quantity γ_m,n is purely real and is equal to the attenuation constant, α_m,n. The amplitude of the component then decreases exponentially. The frequency is below cut-off and the wave does not propagate. The dominant mode of the oscillation is the mode that has the minimum cut-off frequency. When γ_m,n is imaginary the phase of the wave varies with distance z and the wave is propagated with no attenuation. In practice γ_m,n is never purely imaginary and some attenuation always occurs due to energy losses in the transmission line. The effects of different m,n modes on the configuration of a wave travelling along a waveguide can be seen from the diagrams. A waveguide that is designed to separate different modes of oscillation of a wave is termed a mode filter.
2. In signal statistics, the average value computed for each signal data point by taking it and a fixed number of its immediate neighbours and determining the mode value. The mode is the value that occurs most often.

Geology and Earth Sciences

1. The percentage by volume of each of the minerals which make up an igneous rock. Occasionally the term is also applied to metamorphic rocks.
2. In statistics, the average as defined by the most frequently occurring value in a data set.

Philosophy

Term used in scholastic philosophy for a determination, a focusing of being in the abstract into some specific form. In the modern era the term is made prominent by Locke (Essay, ii. 12). Modes are introduced as one kind of complex idea, and are distinguished into simple modes, which are ‘different combinations of the same simple idea’ (Locke cites numbers, such as a dozen or a score), and mixed modes, which are ‘compounded of simple ideas of several kinds, put together to make one complex one’ (Locke cites beauty and theft). Later, fundamental qualities of space, time, and sense are described as simple modes, and mixed modes become ‘scattered and independent ideas, put together by the mind’: again, the central examples remain the ideas connected with action, and moral and legal categories. The idea is that in these areas we can mix ideas to make definitions according to our purposes, whereas in science finding the right words is a matter of tracking the kinds of substances, with their different essences, that independently exist. In Berkeley and Hume there is no distinction between modes and qualities. For Spinoza there is a fundamental distinction between substance and its modes, and ordinary objects are in fact modes of the one real substance, identified equally as the universe, or God.

Economics

The most frequent or most likely value of a random variable. For a discrete probability distribution, the mode is the value that has the highest probability to occur. For a continuous distribution, the mode is the value that corresponds to the maximum of the probability density function; if there is more than one local maximum the distribution is said to be multimodal. For a sample of observations, the mode is the value that is observed most frequently. The number of children in a family, for example, may be 0 or any whole number: if the mode is 2 this means there are more families with two children than of any other particular size.