Suppose that A and B are points in a vertical plane, where B is lower than A but not vertically below A. Imagine a particle starting from rest at A and travelling along a curve from A to B under the force of gravity. The curve with the property that the particle reaches B as soon as possible is called the brachistochrone (from the Greek for ‘shortest time’). The straight line from A to B does not give the shortest time. The required curve is a cycloid, vertical at A and horizontal at B. The problem was posed in 1696 by Jean Bernoulli, and his solution, together with others by Newton, Leibniz and Jacques Bernoulli, was published the following year.

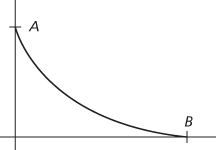
Graph of the brachistochrone