1. (in mathematics) A set of quantities in a rectangular array, used in certain mathematical operations. The array is usually enclosed in large parentheses or in square brackets.
2. (in geology) The fine-grained material of rock in which the coarser-grained material is embedded.
A rectangular array of entries displayed in rows and columns and enclosed in brackets. The entries are elements of some suitable set, either specified or understood. They are often numbers, perhaps integers, real numbers, or complex numbers, but they may be, say, polynomials or other expressions. An m × n matrix has m rows and n columns and can be written
Round brackets may be used instead of square brackets. The subscripts are read as though separated by commas: for example, a23 is read as ‘a, two, three’. The matrix above may be written in abbreviated form as [aij], where the number of rows and columns is understood and aij denotes the entry in the ith row and jth column. See addition (of matrices), block matrix, determinant, diagonal matrix, identity matrix, inverse matrix, matrix groups, matrix of a linear map, multiplication (of matrices), square matrix, trace, transpose, triangular matrix.
An r×c matrix consists of a rectangular array with r rows and c columns, in which the elements are either numbers or algebraic expressions. Example matrices (the plural form) are:
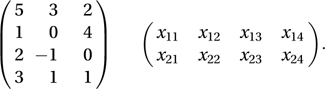 When the array is not written out in full, a matrix is usually denoted by a bold-face capital letter, e.g. X, or by a typical element (or entry) from the array, shown in curly brackets, e.g. {xjk}, where xjk is the element in the jth row and kth column of the matrix. If r=c the matrix is square.
When the array is not written out in full, a matrix is usually denoted by a bold-face capital letter, e.g. X, or by a typical element (or entry) from the array, shown in curly brackets, e.g. {xjk}, where xjk is the element in the jth row and kth column of the matrix. If r=c the matrix is square.If a matrix X={xjk} is multiplied by the real number s, then the result is the matrix sX, in which the element in the jth row and kth column is sxjk. In this context a real number s is often referred to as a scalar.
Two matrices, A and B, can be multiplied together only if the number of columns of one matrix is equal to the number of rows of the other matrix. If A is an m×n matrix and B is an n×p matrix then the product AB is an m×p matrix. However, if p≠m then the product BA does not exist. The rule for the construction of the product is as follows. Let ejk denote the element in the jth row and kth column of the product AB, with ajk and bjk denoting typical elements in A and B. Then ejk is given by
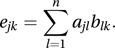
If A and B have the same values of r and c and if ajk=bjk for all j and k, then A=B.
A diagonal matrix is a square matrix with all elements equal to 0, except for those on the leading diagonal (which runs from top-left to bottom-right). This diagonal is also called the main diagonal. A matrix (not necessarily square) in which all the entries are equal on every negatively sloping diagonal is a Toeplitz matrix. For example:

An identity matrix, usually denoted by I, is a diagonal matrix with all leading diagonal elements equal to 1. The size of an identity matrix may be indicated using a suffix: In is an n×n identity matrix.
The transpose of an m×n matrix M is the n×m matrix formed by interchanging the elements of the rows and columns of M. It is denoted by M′. The jth row of M′ is the transpose of the jth column of M and vice versa
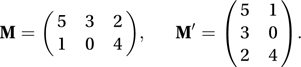 If a square matrix S, with typical element sjk, is equal to its transpose, S′, then it is a symmetric matrix satisfying
If a square matrix S, with typical element sjk, is equal to its transpose, S′, then it is a symmetric matrix satisfying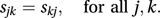
A square matrix that is not symmetric is an asymmetric matrix. If a square matrix S satisfies the equation SS=S then it is idempotent. The product SS may be written as S2. If it exists, the inverse of a square matrix, S, is denoted by S−1. It satisfies the relations that
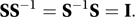
Only square matrices can have an inverse (but see ‘generalized inverse’ below). If S−1 exists then it will be the same size as S. A matrix that has an inverse is said to be non-singular (or regular, or invertible). A square matrix without an inverse is said to be singular.
A square matrix is described as being an upper triangular matrix if all the elements below the leading diagonal are zero, or as a lower triangular matrix if all the elements above the leading diagonal are zero. The matrices U and L are examples:
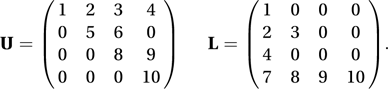 A generalized inverse (also called a Moore–Penrose inverse) of the m×n matrix M is any n×m matrix M− satisfying
A generalized inverse (also called a Moore–Penrose inverse) of the m×n matrix M is any n×m matrix M− satisfying 
If a matrix M is multiplied by its transpose (to give either MM′ or M′M) then the result is a symmetric matrix.
If M is square and the product MM′ is an identity matrix, then M′=M−1 and M is said to be an orthogonal matrix.
A matrix with just one row is called a row vector. A matrix with just one column is called a column vector. Column vectors are usually denoted with a bold-face lower-case letter, e.g. x; row vectors are written as their transpose, e.g. x′. A vector with a single element (i.e. a 1×1 matrix) is a scalar.
Vectors multiply together in the same way as matrices (see above). Thus, if v is an n×1 column vector, and v′ is its transpose, then the product vv′ is an n×n symmetric matrix, and the product v′v is a scalar.
The set of n×1 vectors v1, v2,…, vm is linearly independent if the only values of the scalars a1, a2,…, am for which
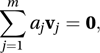 where 0 is an n×1 vector with every element equal to 0, is a1=a2=⋯=am=0. If the set is not linearly independent then it is linearly dependent, in which case there are values for the scalars a1, a2,…, am, not all equal to 0, such that . If a set of two or more vectors is linearly dependent then at least one of the vectors, vk, say, is a linear combination of the others, i.e.
where 0 is an n×1 vector with every element equal to 0, is a1=a2=⋯=am=0. If the set is not linearly independent then it is linearly dependent, in which case there are values for the scalars a1, a2,…, am, not all equal to 0, such that . If a set of two or more vectors is linearly dependent then at least one of the vectors, vk, say, is a linear combination of the others, i.e.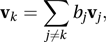 for some scalars b1, b2,…, bk−1, bk+1,…, bm.
for some scalars b1, b2,…, bk−1, bk+1,…, bm.The rank of a matrix is the maximum number of linearly independent rows, which is the same as the maximum number of linearly independent columns. Thus the rank of a matrix is equal to that of its transpose. If a matrix has r rows and c columns, with r≤c, then the rank is≤r; if r>c then the rank is≤c. If the rank is equal to the smaller of r and c then the matrix is of full rank.
If A is a square matrix, x is a column vector not equal to 0, and λ is a scalar such that
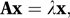 then x is an eigenvector of A and λ is the corresponding eigenvalue. Eigenvectors and eigenvalues are also referred to as characteristic vectors and characteristic values. If x is the column vector (x1 x2…xn)′ and A is an n×n symmetric matrix with typical element ajk, then the product x′Ax, which is a scalar, is described as a quadratic form because it is equal to
then x is an eigenvector of A and λ is the corresponding eigenvalue. Eigenvectors and eigenvalues are also referred to as characteristic vectors and characteristic values. If x is the column vector (x1 x2…xn)′ and A is an n×n symmetric matrix with typical element ajk, then the product x′Ax, which is a scalar, is described as a quadratic form because it is equal to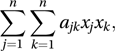 which is a linear combination of all the squared terms (such as x12) and cross-products (such as x1x2).
which is a linear combination of all the squared terms (such as x12) and cross-products (such as x1x2).A symmetric matrix A is a positive definite matrix if x′Ax>0 for all non-zero x; it is a positive semi-definite matrix if x′Ax≥0 for all x and there is at least one non-zero x for which x′Ax=0.
The trace of a square matrix is the sum of the terms on the leading diagonal.
The determinant of a 2×2 square matrix, A, is written as |A| or det(A), and is given by
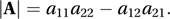
The determinant of a larger matrix is defined recursively in terms of cofactors. The cofactor Ajk of the entry ajk is equal to the product of (−1)j+k and the determinant of the matrix obtained by eliminating the jth row and kth column of A. The recursive definition is . In fact if k=l (otherwise the sum is 0). Similarly, if j=l and is otherwise 0. Thus, for a 3×3 matrix, A,
The eigenvalues of a square matrix A are the roots of the characteristic equation
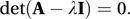
1. (in chemistry) A continuous solid phase in which particles (atoms, ions, etc.) are embedded. Unstable species, such as free radicals, can be trapped in an unreactive substrate, such as solid argon, and studied by spectroscopy. The species under investigation are separated by the matrix, hence the term matrix isolation for this technique.
2. (in geology) The fine-grained material of rock in which the coarser-grained material is embedded.
3. (in mathematics) A set of quantities in a rectangular array, used in certain mathematical operations. The array is usually enclosed in large parentheses or in square brackets.
1. A solid substance within which another substance is embedded such as a metal that constitutes the major part of an alloy.
2. A rock material within which a mineral is embedded.
3. In algebra, a rectangular array of elements set out in rows and columns used to facilitate the solution to mathematical problems. They can be used to present the coefficients of simultaneous linear equations in which each row corresponds to one equation.
A two-dimensional array. In computing, matrices are usually considered to be special cases of n-dimensional arrays, expressed as arrays with two indices. The notation for arrays is determined by the programming language. The two dimensions of a matrix are known as its rows and columns; a matrix with m rows and n columns is said to be an m×n matrix.
In mathematics (and in this dictionary), the conventional notation is to use a capital letter to denote a matrix in its entirety, and the corresponding lower-case letter, indexed by a pair of subscripts, to denote an element in the matrix. Thus the i,jth element of a matrix A is denoted by aij, where i is the row number and j the column number.
A deficient two-dimensional array, in which one of the dimensions has only one index value (and is consequently elided), is a special kind of matrix known either as a row vector (with the column elided) or column vector (with the row elided). The distinction between row and column shows that the two dimensions are still significant.
A rectangular table of numbers, with rows and columns. A matrix M with r rows and c columns is described as being an r × c matrix and would appear as:
where mij denotes the number in the ith row at the jth column position, for i in the range 1..r and j in the range 1..c. A vector is a matrix in which either r or c is equal to 1.
Some arithmetic operators can be extended to work on matrices. Two matrices with the same number of rows and columns can be added by simply adding the numbers in the same row and column positions. Two matrices A and B can be multiplied if the number of columns in A is equal to the number of rows in B. The resulting matrix has the same number of rows as A and the same number of columns as B, with each entry obtained by doing a vector product of rows from A by columns from B.
Matrices can be used to represent transformations within and between coordinate systems, for modelling linear systems, and in finite element methods.
(in histology) The component of tissues (e.g. bone and cartilage) in which the cells of the tissue are embedded. See also extracellular matrix.
1. With respect to a formula in prenex normal form, the quantifier-free formula following the string of quantifiers. For example, for a first-order formula of the form:
•
where each is a universal or existential quantifier, the quantifier-free subformula is the matrix of the formula.
2. A tuple where is nonempty that form the basis for many truth functional semantics. In this setting, a matrix (or logical matrix) is defined so that:
• is a set of truth values
• is a set of designated values
• for all , is a truth function from to for some .
A propositional logic that has a matrix semantics can be interpreted by valuations from the language of that logic to the set of truth values . Such valuations are generally constructed recursively by initially assigning a value for each atomic formula, i.e., so that for all , , and extending throughout the language by means of schema corresponding to the truth conditions for each connective. For every -ary connective , such that is a formula with as its main connective and an -ary truth function interpreting , such a condition is represented as:
•
For logics with matrix semantics, the semantic consequence relation and validity are frequently defined as the preservation of designated values in all valuations, i.e.,
• if for all valuations , if for each then
Logical matrices can be generalized to provide accounts of quantifiers by providing each quantifier a function from to .
The study of whether particular deductive systems can be provided a matrix semantics with finite sets of truth values has been a frequent topic of research. For example, it is an important theorem that intuitionistic logic cannot be characterized by a finite matrix. The introduction of nondeterministic semantics that employ nondeterministic matrices, however, has provided nondeterministic semantics with finitely many values for systems for which there is no finite deterministic matrix.
Lithologic or petrographic term denoting the interstitial material lying between larger crystals, fragments, or particles. It is the background material of small particles in which larger particles and fragments occur. The term is applied to sedimentary rocks; the igneous equivalent is groundmass, although ‘matrix’ is also commonly used of igneous rocks.
See landscape matrix.
- oxytocin
- Oyashio current
- ozonation
- ozone
- ozone hole
- ozone layer
- ozonesonde
- ozonides
- ozonolysis
- O’Brien, Smith
- O’Connell, Daniel (1775–1847)
- O’Connor, Feargus Edward (1794–1855)
- O’Higgins, Bernardo (c.1778–1842)
- P
- p
- p21
- P2P
- p53
- PA
- Pa
- Paasche, Hermann (1851–1925)
- Paasche index
- Paasche price index
- PABX
- PAC