A typical matching problem is as follows: ‘There are n stockbrokers, each wearing his own bowler hat. On arrival at work, each stockbroker leaves his hat in the cloakroom. On leaving work, however, each stockbroker is given a randomly chosen hat by the cloakroom attendant. What is the probability that at least one stockbroker is given his own hat?’ Using the inclusion-exclusion principle, the answer is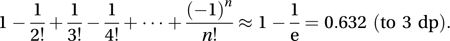Convergence is so quick (n=6 gives 0.632 to 3 dp) that the answer is almost unaffected by the number of stockbrokers. See also secretary problem.